X. Instanciation▲
Imaginons que vous avez une scène représentant de nombreux modèles, mais que la plupart utilisent les mêmes données de sommets. Par exemple, une scène avec des brins d’herbe : chaque brin est un petit modèle de quelques triangles. Vous voudriez probablement en dessiner beaucoup, votre scène contiendrait alors des milliers ou des dizaines de milliers de brins d’herbe à afficher à chaque image. Comme chaque brin contient quelques triangles, un brin s’affiche quasiment instantanément, mais l’ensemble de ces milliers d’appels de rendu réduiraient les performances de manière critique.
Si nous souhaitons afficher un grand nombre d’objets, nous aurions un code comme suit :
for(unsigned int i = 0; i < nombre_de_modele_a_dessiner; i++)
{
DoSomePreparations(); // lier les VAO, les textures, définir les variables uniformes…
glDrawArrays(GL_TRIANGLES, 0, nombre_de_sommets);
}Lors de l’affichage de beaucoup d’instances de votre objet, vous allez sûrement atteindre une baisse de performances à cause du grand nombre d’appels de rendu. En comparaison de l’affichage des sommets, indiquer au GPU de dessiner des données de sommets avec une fonction comme glDrawArrays() ou glDrawElements() consomme beaucoup de temps de calcul, car OpenGL doit faire un travail préparatoire avant de pouvoir dessiner les sommets (comme dire au GPU dans quel tampon lire, où trouver les attributs et toutes ces choses utilisant le bus CPU vers GPU, d’une lenteur inimaginable). Même si le rendu des sommets est ultra-rapide, le fait de donner des commandes de rendu au GPU ne l’est pas.
Il serait pratique si nous pouvions envoyer des données au GPU une seule fois et dire à OpenGL de dessiner les objets plusieurs fois avec un seul appel de rendu. C’est le principe de l’instanciation.
L’instanciation est une technique où nous dessinons plusieurs objets avec un seul appel de rendu, économisant des communications CPU vers GPU pour chaque rendu de cet objet. Celles-ci n’ont besoin d’être effectuées qu’une fois. Pour effectuer un rendu avec l’instanciation, nous devons juste changer nos appels de rendu pour passer de glDrawArrays() et glDrawElements() à glDrawArraysInstanced() et glDrawElementsInstanced(). Ces versions avec instanciation prennent un paramètre supplémentaire, le nombre d’instances (instance count) à afficher. Nous souhaitons donc envoyer toutes les données nécessaires au GPU une seule fois et dire au GPU comment il doit dessiner toutes ces instances en une fois. Le GPU va ensuite afficher ces instances sans devoir communiquer avec le CPU.
En elle-même, cette fonction est inutile. Le rendu d’un même objet un millier de fois est inutile si chaque objet est affiché exactement de la même façon et, donc à la même position ; nous voulons voir plus d’un objet ! Pour cela, le GLSL fournit une autre variable dans le vertex shader : gl_InstanceID.
Lors d’un rendu avec instanciation, la variable gl_InstanceID, démarrant à 0, est incrémentée à chaque instance. Si nous sommes en train d’afficher la 43e instance, la variable gl_InstanceID aurait pour valeur 42 dans le vertex shader. En ayant une valeur unique par instance, nous pouvons l’utiliser comme index pour un grand tableau de positions contenant la position dans le monde de chaque instance.
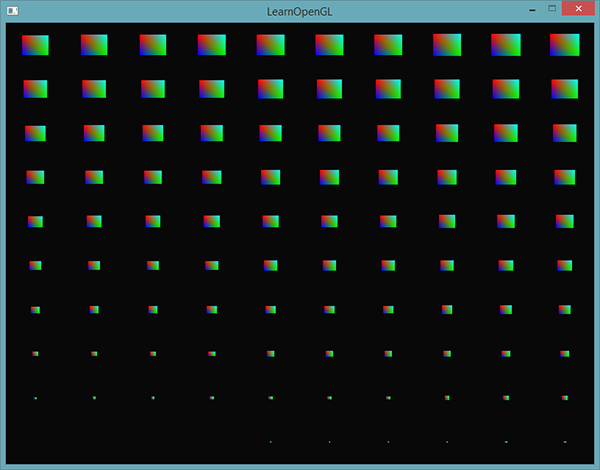
Pour comprendre le rendu instancié, nous allons prendre un exemple simple où nous affichons une centaine de carrés 2D en coordonnées normalisées avec un seul appel. Pour réussir cela, nous allons ajouter un petit décalage à chaque carré en indexant un tableau de variable uniforme de 100 vecteurs. Le résultat forme une grille remplissant l’intégralité de la fenêtre :
Chaque carré est composé de six sommets formant deux triangles. Chaque sommet contient une position 2D en coordonnée normalisée et une couleur. Ci-dessous le tableau des sommets utilisés pour cet exemple. Les triangles sont plutôt petits afin d’en faire rentrer beaucoup dans l’écran :
float quadVertices[] = {
// positions // couleurs
-0.05f, 0.05f, 1.0f, 0.0f, 0.0f,
0.05f, -0.05f, 0.0f, 1.0f, 0.0f,
-0.05f, -0.05f, 0.0f, 0.0f, 1.0f,
-0.05f, 0.05f, 1.0f, 0.0f, 0.0f,
0.05f, -0.05f, 0.0f, 1.0f, 0.0f,
0.05f, 0.05f, 0.0f, 1.0f, 1.0f
};La couleur des carrés est obtenue grâce au fragment shader qui reçoit la couleur transférée par le vertex shader :
#version 330 core
out vec4 FragColor;
in vec3 fColor;
void main()
{
FragColor = vec4(fColor, 1.0);
}Rien de nouveau, mais le vertex shader contient quelque chose d’intéressant :
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
out vec3 fColor;
uniform vec2 offsets[100];
void main()
{
vec2 offset = offsets[gl_InstanceID];
gl_Position = vec4(aPos + offset, 0.0, 1.0);
fColor = aColor;
}Ici, nous avons un tableau de variables uniformes nommé offset qui contient 100 vecteurs pour les décalages. Dans le vertex shader, nous récupérons le vecteur de décalage pour chaque instance grâce à la variable gl_InstanceID. Si nous dessinons 100 carrés, nous obtiendrons 100 carrés placés à différents endroits grâce à ce simple vertex shader.
Nous devons définir les décalages, que nous calculons dans une boucle avant la boucle d’affichage :
glm::vec2 translations[100];
int index = 0;
float offset = 0.1f;
for(int y = -10; y < 10; y += 2)
{
for(int x = -10; x < 10; x += 2)
{
glm::vec2 translation;
translation.x = (float)x / 10.0f + offset;
translation.y = (float)y / 10.0f + offset;
translations[index++] = translation;
}
}Ainsi, nous créons 100 vecteurs permettant de positionner les objets sur une grille de taille 10x10. En plus de la génération du tableau, nous devons transférer les données au tableau de variables uniformes du vertex shader :
shader.use();
for(unsigned int i = 0; i < 100; i++)
{
stringstream ss;
string index;
ss << i;
index = ss.str();
shader.setVec2(("offsets[" + index + "]").c_str(), translations[i]);
}Grâce à ce code, nous transformons le compteur i de la boucle en une chaîne de caractères afin de l’utiliser comme nom de variable uniforme. Pour chaque élément du tableau de variables uniformes offsets, nous lui assignons son vecteur correspondant.
Maintenant que nous avons préparé la scène, nous pouvons afficher les carrés. Pour les dessiner, nous appelons glDrawArraysInstanced() ou glDrawElementsInstanced(). Comme nous n’utilisons pas de tampon d’éléments, nous allons utiliser la fonction glDrawArraysInstanced() :
glBindVertexArray(quadVAO);
glDrawArraysInstanced(GL_TRIANGLES, 0, 6, 100);Les paramètres de la fonction glDrawArraysInstanced() sont exactement les mêmes que glDrawArrays() sauf pour le dernier paramètre, indiquant le nombre d’instances à dessiner. Comme nous voulons afficher 100 carrés sur une grille de 10x10, nous passons 100 en argument. En exécutant ce code, vous devriez obtenir une image familière de 100 carrés colorés.
X-A. Tableaux instanciés▲
Bien que l’implémentation précédente fonctionne pour ce cas précis, nous souhaitons instancier plus de 100 instances (ce qui est classique). Nous allons certainement atteindre une limite sur le nombre de variables uniformes que nous pouvons passer au shader. Une autre alternative est d’appeler un tableau instancié (instanced array) défini comme un attribut de sommets (et nous permettant de passer plus de données) qui n’est mis à jour que lorsque le vertex shader affiche une nouvelle instance.
Avec les attributs de sommets, chaque exécution du vertex shader provoquera la récupération du prochain attribut de sommet correspondant au sommet actuel. Lors de la définition d’un attribut de sommets tel qu’un tableau instancié, le vertex shader met à jour uniquement le contenu de l’attribut de sommet par instance et non plus par sommet. Cela permet d’utiliser un attribut de sommet standard pour les données des sommets et un tableau instancié pour les données des instances.
Pour vous donner un exemple d’un tableau instancié, nous allons reprendre l’exemple précédent et passer les décalages à travers un tableau instancié. Nous devons mettre à jour le vertex shader pour ajouter un nouvel attribut :
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
layout (location = 2) in vec2 aOffset;
out vec3 fColor;
void main()
{
gl_Position = vec4(aPos + aOffset, 0.0, 1.0);
fColor = aColor;
}Nous n’utilisons plus la variable gl_InstanceID et nous pouvons directement utiliser l’attribut offset sans avoir à l’indexer à partir d’un quelconque tableau.
Comme le tableau instancié est un attribut de sommet, tout comme les variables position et color, nous devons stocker son contenu dans un tampon de sommet et le configurer avec un pointeur d’attribut de sommets. Nous commençons par stocker le tableau translations (de la section précédente) dans un nouveau tampon :
unsigned int instanceVBO;
glGenBuffers(1, &instanceVBO);
glBindBuffer(GL_ARRAY_BUFFER, instanceVBO);
glBufferData(GL_ARRAY_BUFFER, sizeof(glm::vec2) * 100, &translations[0], GL_STATIC_DRAW);
glBindBuffer(GL_ARRAY_BUFFER, 0);Ensuite, nous devons définir le pointeur d’attribut de sommet et activer cet attribut :
glEnableVertexAttribArray(2);
glBindBuffer(GL_ARRAY_BUFFER, instanceVBO);
glVertexAttribPointer(2, 2, GL_FLOAT, GL_FALSE, 2 * sizeof(float), (void*)0);
glBindBuffer(GL_ARRAY_BUFFER, 0);
glVertexAttribDivisor(2, 1);Ce code est intéressant grâce à l’appel à l’apparition de la fonction glVertexAttribDivisor(). Celle-ci indique à OpenGL quand mettre à jour le contenu de l’attribut de sommet avec le prochain élément. Le premier paramètre est l’attribut de sommets et le second est le diviseur d’attribut (attribute divisor). Par défaut, le diviseur est 0, qui indique à OpenGL de mettre à jour l’attribut de sommet à chaque itération dans le vertex shader. En définissant l’attribut à 1, nous indiquons à OpenGL que nous voulons mettre à jour le contenu de l’attribut de sommets lorsque nous démarrons une nouvelle instance. En le définissant à 2, le contenu est mis à jour toutes les deux instances et ainsi de suite. Ici, nous le mettons à 1 pour indiquer à OpenGL que l’attribut de sommets à l’emplacement 2 est un tableau instancié.
Si nous affichons les carrés maintenant, nous obtiendrions le même résultat :
C’est exactement le même résultat que précédemment, mais, cette fois, nous avons utilisé les tableaux instanciés, ce qui nous permet de passer plus de données (autant que nous avons de mémoire) au vertex shader pour le rendu instancié.
Pour nous amuser, nous pouvons aussi réduire lentement la taille de chaque carré en partant du haut et de la droite avec gl_InstanceID. Pourquoi pas ?
void main()
{
vec2 pos = aPos * (gl_InstanceID / 100.0);
gl_Position = vec4(pos + aOffset, 0.0, 1.0);
fColor = aColor;
}Le résultat est que les premières instances du carré sont dessinées très petit et plus nous progressons dans le processus de rendu, plus la variable gl_InstanceID s’approche de 100 et donc plus les carrés retrouvent leur taille originale. C’est parfaitement possible d’utiliser les tableaux instanciés en même temps que la variable gl_InstanceID.
Si vous ne voyez toujours pas comment le rendu instancié fonctionne ou que vous souhaitez voir comment le tout s’assemble, vous pouvez trouver le code source de l’application ici.
Même si c’est amusant, ces exemples ne sont pas de bons exemples pour l’instanciation. Oui, cela donne un bon aperçu du fonctionnement de l’instanciation, mais celle-ci est vraiment utile lors de l’affichage d’un très grand nombre d’objets similaires, ce que nous n’avons jamais fait jusqu’à présent. Pour cette raison, nous allons nous aventurer dans l’espace et voir la vraie puissance du rendu instanciée.
X-B. Affichage d’un champ d’astéroïdes▲
Imaginez une scène où nous avons une très grande planète entourée par un énorme champ d’astéroïdes. Un tel anneau d’astéroïdes doit contenir des milliers et des centaines de milliers de cailloux : il devient donc très rapidement impossible à afficher pour une carte graphique décente. Le scénario s’avère être le terrain propice pour le rendu instancié, car les astéroïdes peuvent provenir d’un seul modèle. Chaque astéroïde contient seulement quelques petites variations à travers la matrice de transformations, une matrice unique à chaque astéroïde.
Pour montrer l’impact du rendu instancié, nous allons d’abord afficher la scène avec des astéroïdes autour de la planète, mais sans rendu instancié. La scène ne contiendra qu’un modèle de planète qui peut être téléchargé ici et un grand ensemble d’astéroïdes positionnés autour de la planète. Le modèle pour l’astéroïde peut être téléchargé ici.
Grâce au code vu dans le tutoriel sur le chargement des modèles, nous chargeons les modèles pour cette scène.
Pour réussir cet effet, nous allons générer la matrice de transformation pour chaque astéroïde. La matrice de transformation est créée en déplaçant l’astéroïde dans l’anneau – puis en ajoutant un petit déplacement pour obtenir un effet plus naturel. Ensuite, nous appliquons un petit redimensionnement et une petite rotation. Le résultat est une matrice de transformation pour placer chaque astéroïde quelque part autour de la planète, tout en ajoutant un petit plus pour donner un aspect naturel et unique par rapport aux autres astéroïdes. Le résultat est un anneau plein d’astéroïdes où chaque astéroïde est différent des autres.
unsigned int amount = 1000;
glm::mat4 *modelMatrices;
modelMatrices = new glm::mat4[amount];
srand(glfwGetTime()); // initialiser la graine de la génération aléatoire
float radius = 50.0;
float offset = 2.5f;
for(unsigned int i = 0; i < amount; i++)
{
glm::mat4 model;
// 1. translation : déplacer autour d’un cercle de rayon 'radius' dans l’espace [-offset, offset]
float angle = (float)i / (float)amount * 360.0f;
float displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
float x = sin(angle) * radius + displacement;
displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
float y = displacement * 0.4f; // garder la taille du champ d’astéroïdes comparé à la largeur de x et z
displacement = (rand() % (int)(2 * offset * 100)) / 100.0f - offset;
float z = cos(angle) * radius + displacement;
model = glm::translate(model, glm::vec3(x, y, z));
// 2. mise à l’échelle : facteur 0.05 et 0.25f
float scale = (rand() % 20) / 100.0f + 0.05;
model = glm::scale(model, glm::vec3(scale));
// 3. rotation : ajoute une rotation aléatoire autour d’un axe de rotation pris (semi)aléatoirement
float rotAngle = (rand() % 360);
model = glm::rotate(model, rotAngle, glm::vec3(0.4f, 0.6f, 0.8f));
// 4. ajout à la liste des matrices
modelMatrices[i] = model;
}Ce morceau de code peut sembler un peu intimidant, mais nous ne faisons que transformer la position x et z de l’astéroïde autour d’un cercle suivant un rayon défini par la variable radius. De plus, l’astéroïde est légèrement déplacé autour du cercle d’un décalage entre -offset et offset. L’impact sur le déplacement en y est légèrement réduit pour donner un aspect plus plat à l’anneau d’astéroïde. Ensuite, nous appliquons un redimensionnement et une rotation puis nous stockons la matrice obtenue dans modelMatrices de la taille amount. Nous générons ici 1 000 matrices, une par astéroïde.
Après avoir chargé les modèles de la planète et de l’astéroïde et compilé l’ensemble des shaders, le code du rendu ressemble à :
// dessiner la planète
shader.use();
glm::mat4 model;
model = glm::translate(model, glm::vec3(0.0f, -3.0f, 0.0f));
model = glm::scale(model, glm::vec3(4.0f, 4.0f, 4.0f));
shader.setMat4("model", model);
planet.Draw(shader);
// dessiner les astéroïdes
for(unsigned int i = 0; i < amount; i++)
{
shader.setMat4("model", modelMatrices[i]);
rock.Draw(shader);
}Premièrement, nous dessinons la planète que nous déplaçons et redimensionnons pour que cela corresponde mieux à la scène, puis nous dessinons les 1000 astéroïdes avec les matrices que nous avons calculées. Toutefois, avant de dessiner chaque astéroïde, nous définissons la matrice de transformation dans le shader.
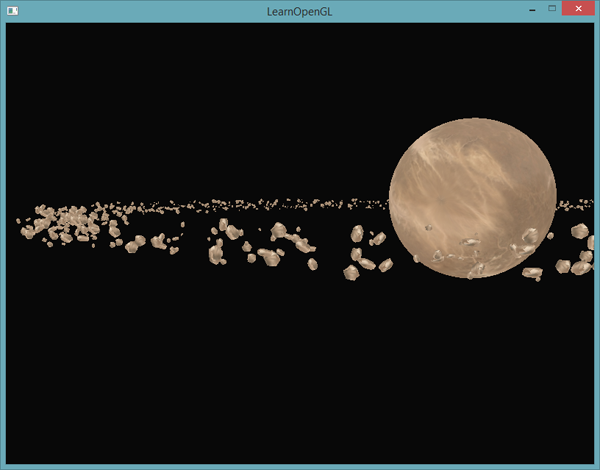
Le résultat donne une scène spatiale où nous pouvons voir un anneau d’astéroïdes presque naturel autour de la planète :
La scène nécessite au total 1001 appels de rendu par image, dont 1000 pour les astéroïdes. Vous pouvez trouver le code source de cette scène ici.
Aussitôt que nous augmentons le nombre, nous pouvons remarquer que la scène n’est plus fluide et que le nombres d’images par seconde diminue fortement. Dès que nous passons à 2000 astéroïdes, la scène devient tellement lente qu’il est impossible de s’y déplacer.
Essayons maintenant d’afficher la même scène, mais en utilisant le rendu instanciés. Nous allons d’abord adapter le vertex shader :
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 2) in vec2 aTexCoords;
layout (location = 3) in mat4 instanceMatrix;
out vec2 TexCoords;
uniform mat4 projection;
uniform mat4 view;
void main()
{
gl_Position = projection * view * instanceMatrix * vec4(aPos, 1.0);
TexCoords = aTexCoords;
}Nous n’allons plus utiliser la variable uniforme : nous la remplaçons par une variable de type mat4 comme attribut de sommet. Ainsi, on pourra stocker un tableau instancié pour les matrices de transformation. Toutefois, nous utilisons, comme attribut de sommets, un type de données plus grand qu’un vec4 et qui s’utilise un peu différemment. Le nombre maximum de données permise par un attribut de sommet correspond à vec4. Comme un mat4 n’est que quatre vec4, nous avons réservé quatre attributs de sommets pour cette matrice. Sachant que le premier vec4 est à l’emplacement 3, les colonnes de la matrice seront aux emplacements 3, 4, 5 et 6.
Ensuite, nous devons définir chaque pointeur d’attributs pour ces quatre attributs de sommets et les configurer comme tableau instancié :
// tampons de sommets
unsigned int buffer;
glGenBuffers(1, &buffer);
glBindBuffer(GL_ARRAY_BUFFER, buffer);
glBufferData(GL_ARRAY_BUFFER, amount * sizeof(glm::mat4), &modelMatrices[0], GL_STATIC_DRAW);
for(unsigned int i = 0; i < rock.meshes.size(); i++)
{
unsigned int VAO = rock.meshes[i].VAO;
glBindVertexArray(VAO);
// attributs de sommet
GLsizei vec4Size = sizeof(glm::vec4);
glEnableVertexAttribArray(3);
glVertexAttribPointer(3, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)0);
glEnableVertexAttribArray(4);
glVertexAttribPointer(4, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(vec4Size));
glEnableVertexAttribArray(5);
glVertexAttribPointer(5, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(2 * vec4Size));
glEnableVertexAttribArray(6);
glVertexAttribPointer(6, 4, GL_FLOAT, GL_FALSE, 4 * vec4Size, (void*)(3 * vec4Size));
glVertexAttribDivisor(3, 1);
glVertexAttribDivisor(4, 1);
glVertexAttribDivisor(5, 1);
glVertexAttribDivisor(6, 1);
glBindVertexArray(0);
}Notez que vous pouvez tricher en déclarant le VAO de la classe Mesh comme variable publique au lieu d’une variable privée, ce qui permet d’y accéder avec un tableau de sommets. Ce n’est pas la solution la plus propre, mais juste une modification pour correspondre à ce tutoriel. Mis à part cette petite astuce, le code doit être évident. Nous avons défini comment OpenGL doit interpréter le tampon pour chaque attribut de sommets de la matrice et pour chaque attribut de sommets, un tableau instancié.
Ensuite, nous prenons le VAO du modèle une nouvelle fois et nous les dessinons avec la fonction glDrawElementsInstanced() :
// dessiner les astéroïdes
instanceShader.use();
for(unsigned int i = 0; i < rock.meshes.size(); i++)
{
glBindVertexArray(rock.meshes[i].VAO);
glDrawElementsInstanced(
GL_TRIANGLES, rock.meshes[i].indices.size(), GL_UNSIGNED_INT, 0, amount
);
}Maintenant, nous dessinons le même nombre d’astéroïdes que dans l’exemple précédent, mais cette fois, à l’aide du rendu instancié. Le résultat doit être similaire, mais dès que vous commencez à augmenter le nombre grâce à la variable amount vous voyez l’effet de l’instanciation. Sans rendu instancié, nous étions capable d’afficher 1000 à 1500 astéroïdes sans problème. Avec le rendu instancié nous pouvons définir cette valeur à 100 000. Le modèle d’astéroïde possède 576 sommets : la scène contient 57 millions de sommets, affichés à chaque image, sans perte de performance !
Cette image a été affichée avec 100 000 astéroïdes dans un rayon de 150,0 et un décalage de 25,0. Vous pouvez trouver le code source de cette démo de rendu instancié ici.
Sur certaines machines, un nombre de 100 000 astéroïdes peut être trop haut, essayez donc des valeurs plus faibles pour obtenir un rendu acceptable.
Comme vous pouvez le voir, avec le bon environnement, l’instanciation peut permettre une énorme différence dans les capacités de rendu de votre carte graphique. Pour cela, l’instanciation est couramment utilisée pour l’herbe, la flore, les particules et les scènes comme celle-ci – soit, pour n’importe quelle scène ayant un grand nombre de formes se répétant.
X-C. Remerciements▲
Ce tutoriel est une traduction réalisée par Alexandre Laurent dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.