IX. Geometry shader▲
Il existe une étape optionnelle entre le vertex shader et le fragment shader appelée le geometry shader. Un geometry shader prend en entrée un ensemble de sommets formant une primitive simple, c’est-à-dire un point ou un triangle, qu’il peut ensuite transformer à sa guise avant de l’envoyer à l’étape du pipeline qui suit. Les geometry shaders sont intéressants, car ils permettent de transformer l’ensemble des sommets en une primitive complètement différente et, pourquoi pas, d’ajouter d’autres sommets à ceux donnés.
Nous allons directement commencer par un exemple d’un geometry shader :
#version 330 core
layout (points) in;
layout (line_strip, max_vertices = 2) out;
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
}Au début de tout geometry shader, nous devons déclarer le type de primitive en entrée envoyée par le vertex shader. Nous le faisons en déclarant une disposition devant le mot clé in. Cet indicateur de disposition peut prendre une des valeurs suivantes :
- points : lors de l’affichage des primitives GL_POINTS (1) ;
- lines : lors de l’affichage avec GL_LINES ou GL_LINE_STRIP (2) ;
- lines_adjacency : GL_LINES_ADJACENCY ou GL_LINE_STRIP_ADJACENCY (4) ;
- triangles : GL_TRIANGLES, GL_TRIANGLE_STRIP ou GL_TRIANGLE_FAN (3) ;
- triangles_adjacency : GL_TRIANGLES_ADJACENCY ou GL_TRIANGLE_STRIP_ADJACENCY (6).
En bref, cela reflète les primitives que nous pouvons spécifier lors de l’appel à glDrawArrays(). Si nous choisissons de dessiner des GL_TRIANGLES, nous devrions choisir le qualificateur triangles. Le nombre entre parenthèses représente le nombre minimum de sommets que chaque primitive contient.
Ensuite, nous devons aussi indiquer le type de primitive que le geometry shader génère et nous le faisons en ajoutant un qualificateur de disposition au mot-clé out. Comme pour les entrées, le qualificateur de sortie peut prendre une de ces valeurs :
- points ;
- line_strip ;
- triangle_strip.
Avec juste ces trois qualificateurs de sorties, nous pouvons créer toutes les formes que nous voulons à partir des primitives d’entrée. Pour générer un simple triangle, nous pouvons utiliser triangle_strip comme sortie et générer trois sommets.
Le geometry shader attend aussi que nous définissions le nombre de sommets maximal en sortie (si vous dépassez ce nombre, OpenGL ne dessinera pas les sommets supplémentaires), ce que nous pouvons faire dans le qualificateur de disposition du mot-clé out. Dans ce cas, nous allons utiliser une sortie line_strip avec un maximum de deux sommets.
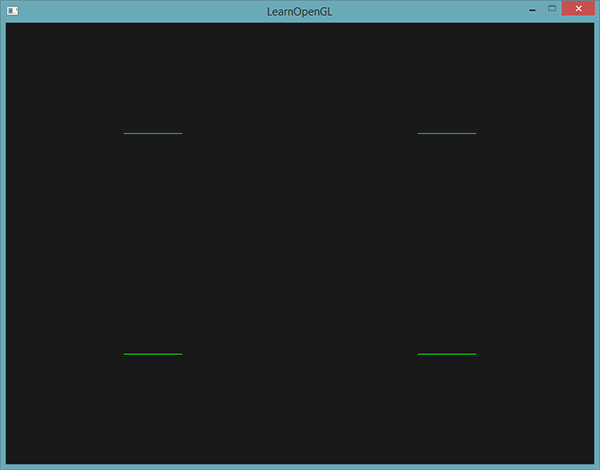
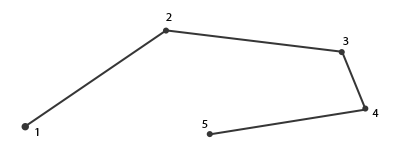
Au cas où vous vous posez la question : un line_strip est un ensemble de lignes connectées ensemble permettant de former une ligne continue constituée au minimum par deux points. Chaque point supplémentaire permet de créer une nouvelle ligne entre le nouveau point et le point précédent, comme vous pouvez le voir dans l’image ci-dessous, avec cinq sommets :
Avec le shader actuel, nous allons afficher une simple ligne avec un nombre maximal de deux sommets.
Pour générer des résultats adéquats, nous devons trouver un moyen de récupérer la sortie de l’étape précédente du pipeline. Le GLSL nous propose la variable gl_in qui, en interne, ressemble (sûrement) à ceci :
in gl_Vertex
{
vec4 gl_Position;
float gl_PointSize;
float gl_ClipDistance[];
} gl_in[];C’est un bloc d’interface (comme vu dans le tutoriel précédent) qui contient quelques variables intéressantes, notamment gl_Position, qui contient un vecteur similaire à celui en sortie du vertex shader.
Notez que c’est un tableau, car la plupart des primitives contiennent plus d’un sommet et que le geometry shader reçoit tous les sommets en une entrée.
En utilisant les données des sommets provenant du vertex shader, nous pouvons générer de nouvelles données grâce à deux fonctions du geometry shader : EmitVertex et EndPrimitive. Le geometry shader attend que vous génériez au moins une primitive que vous avez spécifiée en sortie. Dans notre cas, nous devons générer au moins une primitive de type line_strip.
void main() {
gl_Position = gl_in[0].gl_Position + vec4(-0.1, 0.0, 0.0, 0.0);
EmitVertex();
gl_Position = gl_in[0].gl_Position + vec4( 0.1, 0.0, 0.0, 0.0);
EmitVertex();
EndPrimitive();
}Chaque fois que nous appelons la fonction EmitVectex(), le sommet actuellement défini dans la variable gl_Position est ajouté à la primitive. Chaque fois que la fonction EndPrimitive() est appelée, tous les sommets de cette primitive sont combinés pour former la primitive à afficher. En appelant EndPrimitive() plusieurs fois après les appels à EmitVertex(), plusieurs primitives peuvent être générées. Dans ce cas particulier, nous émettons deux sommets ayant un petit décalage par rapport à la position du sommet original. Ensuite, l’appel à la fonction EndPrimitive() permet de combiner ces deux sommets en une suite de lignes de deux sommets.
Maintenant que vous savez (en quelque sorte) comment le geometry shader fonctionne, vous avez certainement deviné ce qu’il fait. Le geometry shader prend des points en entrée et crée une ligne horizontale avec le point en entrée comme centre. Cela donne le résultat visuel suivant :
Ce n’est pas incroyable pour le moment, mais il ne faut pas oublier que cela a été généré avec l’appel de rendu suivant :
glDrawArrays(GL_POINTS, 0, 4);Même si c’est un exemple simple, cela montre comment utiliser les geometry shaders et comment générer (dynamiquement) de nouvelles formes. Plus tard dans ce tutoriel, nous allons voir comment créer des effets intéressants avec les geometry shaders. Avant, nous allons toutefois créer un geometry shader simple.
IX-A. Utiliser les geometry shaders▲
Pour montrer l’utilisation du geometry shader, nous allons afficher une scène simple où nous dessinons quatre points sur le plan Z dans les coordonnées normalisées du périphérique. Les coordonnées de ces points sont :
float points[] = {
-0.5f, 0.5f, // haut gauche
0.5f, 0.5f, // haut droit
0.5f, -0.5f, // bas droit
-0.5f, -0.5f // bas gauche
};Le vertex shader n’a besoin que de dessiner les points sur le plan Z, nous avons donc besoin d’un vertex shader basique :
#version 330 core
layout (location = 0) in vec2 aPos;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
}Nous donnons une couleur verte pour chaque point dans le fragment shader :
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(0.0, 1.0, 0.0, 1.0);
}Vous devez générer le VAO et le VBO des points, puis les dessiner avec ce code :
shader.use();
glBindVertexArray(VAO);
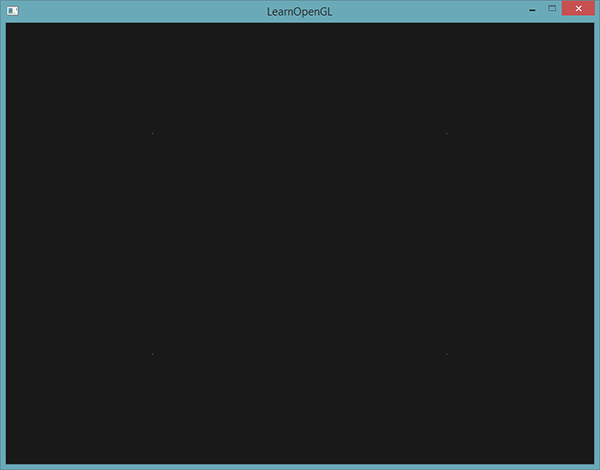
glDrawArrays(GL_POINTS, 0, 4);Le résultat donne une scène noire avec quatre points verts (difficiles à voir) :
Mais nous avons déjà appris tout cela ? Oui, et maintenant nous allons pimenter un peu cette scène en lui ajoutant un geometry shader.
Pour les besoins de l’apprentissage, nous allons créer un geometry shader de transfert (pass-through) qui prend la primitive de point en entrée et qui la passe, non modifiée, au prochain shader du pipeline :
#version 330 core
layout (points) in;
layout (points, max_vertices = 1) out;
void main() {
gl_Position = gl_in[0].gl_Position;
EmitVertex();
EndPrimitive();
}Jusqu’à présent, le geometry shader doit être facile à comprendre. Il émet simplement la position du sommet reçu en entrée et génère un point en sortie.
Le geometry shader doit être compilé et lié dans le programme, comme pour le vertex shader et le fragment shader, mais, cette fois, avec le type est GL_GEOMETRY_SHADER :
geometryShader = glCreateShader(GL_GEOMETRY_SHADER);
glShaderSource(geometryShader, 1, &gShaderCode, NULL);
glCompileShader(geometryShader);
...
glAttachShader(program, geometryShader);
glLinkProgram(program);Le code de compilation du shader est basiquement le même que celui pour le vertex et le fragment shader. Soyez certain de vérifier pour les erreurs de compilation ou d’édition de liens !
Si vous compilez et exécutez le programme, vous devriez obtenir le résultat suivant :
C’est exactement le même résultat que sans le geometry shader ! C’est un peu nul, je l’admets, mais, en réalité, si nous avons toujours nos points, cela signifie que le geometry shader fonctionne. Il est maintenant l’heure de faire des trucs amusants !
IX-B. Construisons des maisons▲
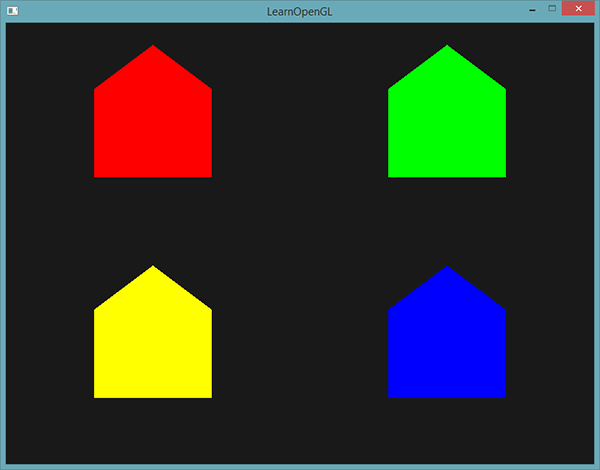
Dessiner des points et des lignes n’est pas très intéressant, alors nous allons être un peu plus créatifs grâce au geometry shader. Nous allons dessiner une maison à l’emplacement de chaque point. Nous pouvons réussir cela en indiquant que le geometry shader doit produire une bande de triangles (triangle_strip) et dessiner trois triangles : deux pour le carré et un pour le toit.
Une bande de triangles en OpenGL est une façon efficace de dessiner des triangles en utilisant moins de sommets. Une fois que le premier triangle est dessiné, chaque sommet qui suit permet de générer un autre triangle à côté du premier : chaque trio de sommets adjacents forme un nouveau triangle. Si nous avons un total de six sommets qui forme une bande de triangles, nous obtiendrons les triangles suivants : (1,2,3), (2,3,4), (3,4,5) et (4,5,6), soit quatre triangles. Une bande de triangles nécessite au moins trois sommets et génère N-2 triangles ; avec six sommets, nous créons 6-2 = 4 triangles. L’image suivante schématise cela :
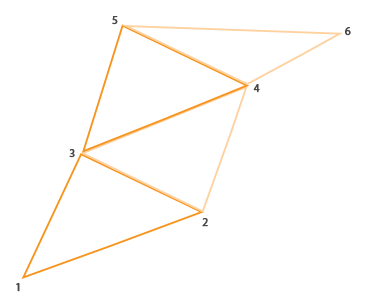
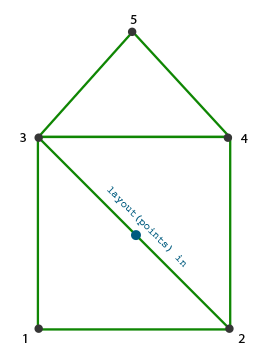
En utilisant une bande de triangles comme sortie du geometry shader, nous pouvons facilement créer une maison avec trois triangles adjacents. L’image suivante montre quel ordre utiliser pour les sommets permettant d’obtenir les triangles dont nous avons besoin. Le point bleu est le point en entrée du geometry shader :
Cela se traduit par le geometry shader suivant :
#version 330 core
layout (points) in;
layout (triangle_strip, max_vertices = 5) out;
void build_house(vec4 position)
{
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1:bottom-left
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2:bottom-right
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3 : haut gauche
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4 : haut droit
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5 :haut
EmitVertex();
EndPrimitive();
}
void main() {
build_house(gl_in[0].gl_Position);
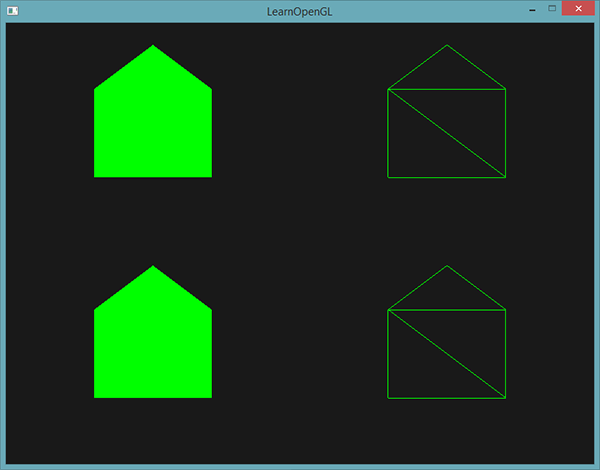
}Le geometry shader génère cinq sommets, en décalant les coordonnées du point d’entrée, pour former une bande de triangles. La primitive résultante est ensuite traitée par le fragment shader qui s’exécute sur l’intégralité de la bande de triangles, donnant ainsi une maison verte pour chaque point dessiné :
Vous pouvez voir que chaque maison comporte trois triangles, tous dessinés en partant d’un point. Les maisons vertes sont un peu ennuyantes : améliorons donc le rendu et donnons une couleur unique à chaque maison. Pour ce faire, nous allons ajouter un attribut de couleur supplémentaire par sommet dans le vertex shader, le transférer au geometry shader, qui va l’envoyer au fragment shader.
Les données des sommets à jour sont comme suit :
float points[] = {
-0.5f, 0.5f, 1.0f, 0.0f, 0.0f, // haut gauche
0.5f, 0.5f, 0.0f, 1.0f, 0.0f, // haut droit
0.5f, -0.5f, 0.0f, 0.0f, 1.0f, // bas droit
-0.5f, -0.5f, 1.0f, 1.0f, 0.0f // bas gauche
};Ensuite, nous mettons à jour le vertex shader pour transférer la couleur au geometry shader grâce au bloc d’interface :
#version 330 core
layout (location = 0) in vec2 aPos;
layout (location = 1) in vec3 aColor;
out VS_OUT {
vec3 color;
} vs_out;
void main()
{
gl_Position = vec4(aPos.x, aPos.y, 0.0, 1.0);
vs_out.color = aColor;
}Nous devons déclarer le même bloc d’interface (avec un nom d’interface différent) dans le geometry shader :
in VS_OUT {
vec3 color;
} gs_in[];Comme le geometry shader agit sur un ensemble de sommets en entrée, les données en entrée sont dans un tableau, même si nous ne traitons qu’un seul sommet.
Nous n’avons pas nécessairement besoin d’utiliser un bloc d’interface pour transférer les données au geometry shader. Nous aurions pu écrire :
in vec3 vColor[];Le vertex shader aurait pu transférer la couleur avec out vec3 vColor. Toutefois, les blocs d’interface sont plus simple à utiliser dans les shaders comme le geometry shader. Dans la pratique, les entrées du geometry shader peuvent être conséquentes et les regrouper dans un grand bloc d’interface est plus logique.
Ensuite, nous devons déclarer une couleur en sortie pour la passer au fragment shader :
out vec3 fColor;Comme le fragment shader attend une seule couleur (interpolée), cela n’est pas logique de transférer plusieurs couleurs. Le vecteur fColor n’est donc pas un tableau, mais un simple vecteur. Lors de l’émission d’un sommet, chaque sommet stocke au moins une fColor pour l’exécution du fragment shader. Pour les maisons, nous allons donner comme valeur à fColor la première couleur qui a été émise par le vertex shader :
fColor = gs_in[0].color; // gs_in[0] comme il n’y a qu’un sommet en entrée
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1 : bas gauche
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2 : bas droit
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3 : haut gauche
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4 : haut droit
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5 : haut
EmitVertex();
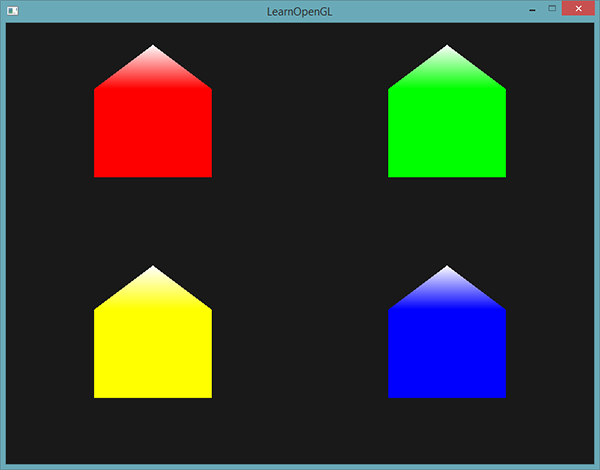
EndPrimitive();Tous les sommets émis contiennent la dernière valeur de fColor, égale à la couleur du sommet définie dans leurs attributs. Toutes les maisons ont maintenant une couleur différente :
Pour nous amuser, nous pouvons imaginer qu’il y a de la neige sur le toit des maisons en donnant une couleur au dernier sommet :
fColor = gs_in[0].color;
gl_Position = position + vec4(-0.2, -0.2, 0.0, 0.0); // 1 : bas gauche
EmitVertex();
gl_Position = position + vec4( 0.2, -0.2, 0.0, 0.0); // 2 : bas droit
EmitVertex();
gl_Position = position + vec4(-0.2, 0.2, 0.0, 0.0); // 3 : haut gauche
EmitVertex();
gl_Position = position + vec4( 0.2, 0.2, 0.0, 0.0); // 4 : haut droit
EmitVertex();
gl_Position = position + vec4( 0.0, 0.4, 0.0, 0.0); // 5 : haut
fColor = vec3(1.0, 1.0, 1.0);
EmitVertex();
EndPrimitive();Le résultat donne quelque chose comme suit :
Vous pouvez trouver le code source ici.
Vous pouvez voir que les geometry shaders permettent des choses créatives avec la plus simple des primitives. Comme la forme est générée dynamiquement sur le matériel ultra-rapide qu’est le GPU, c’est bien plus efficace que de définir des formes par vous-même dans les tampons de sommets. Les geometry shaders sont donc un outil d’optimisation pour les formes simples et répétitives comme les cubes d’un monde en voxel ou les brins d’herbe dans un champ.
IX-C. Exploser les objets▲
Même si afficher des maisons, c’est cool, nous n’allons pas l’utiliser très souvent. C’est pourquoi nous allons monter d’un cran et exploser les objets ! Nous n’allons peut-être pas les utiliser beaucoup, mais cela montre la puissance des geometry shaders.
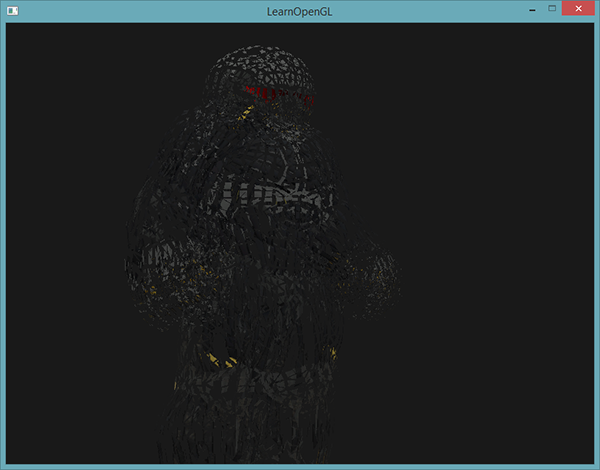
Lorsque nous parlons d’exploser un objet, nous n’allons pas exploser nos précieux sommets empaquetés, mais nous allons déplacer chaque triangle suivant la direction de leur normale sur une petite période de temps. Cet effet semble faire que l’objet explose suivant la direction de la normale. Cela donne le rendu suivant :
La bonne chose avec un tel effet provenant du geometry shader est que cela fonctionne sur tous les objets, quelle que soit leur complexité.
Comme nous allons déplacer tous les sommets dans la direction de la normale de leur triangle, nous devons calculer la normale. Il suffit de calculer un vecteur perpendiculaire à la surface du triangle, à laquelle nous pouvons accéder grâce aux trois sommets. Rappelez-vous ce que nous avons vus dans le tutoriel sur les transformations :vous pouvez obtenir le vecteur perpendiculaire à partir de deux vecteurs, a et b, qui sont parallèles à la surface du triangle. Cela se réalise grâce au produit vectoriel de ces deux vecteurs. Le geometry shader suivant fait exactement cela en obtenant la normale à partir des trois sommets en entrée :
vec3 GetNormal()
{
vec3 a = vec3(gl_in[0].gl_Position) - vec3(gl_in[1].gl_Position);
vec3 b = vec3(gl_in[2].gl_Position) - vec3(gl_in[1].gl_Position);
return normalize(cross(a, b));
}Ici, nous obtenons deux vecteurs a et b parallèles à la surface du triangle grâce à une soustraction. Soustraire deux vecteurs entre eux permet d’obtenir un vecteur qui est la différence. Comme les trois points forme un triangle, la soustraction de n’importe quels vecteurs entre eux donne un vecteur parallèle au plan. Notez que, si nous avions interverti a et b dans la fonction cross(), nous aurions obtenu une normale pointant dans la direction opposée. L’ordre est important ici !
Maintenant que nous savons calculer la normale, nous pouvons écrire une fonction explode() qui prend cette normale ainsi que la position d’un sommet. La fonction retourne un nouveau vecteur, résultant dans le déplacement du vecteur à la suivant la direction de la normale :
vec4 explode(vec4 position, vec3 normal)
{
float magnitude = 2.0;
vec3 direction = normal * ((sin(time) + 1.0) / 2.0) * magnitude;
return position + vec4(direction, 0.0);
}La fonction en elle-même n’est pas compliquée. La fonction sin() reçoit une variable time comme argument, représentant le temps et retourne une valeur entre -1,0 et 1,0. Comme nous ne voulons pas que l’objet implose, nous modifions les valeurs retournées pour qu’elles soient comprises dans l’intervalle [0, 1]. La valeur ainsi obtenue est multipliée par la normale, ce qui donne ainsi une direction, qui est ensuite ajoutée à la position.
Le geometry shader produisant l’effet d’explosion est celui-ci :
#version 330 core
layout (triangles) in;
layout (triangle_strip, max_vertices = 3) out;
in VS_OUT {
vec2 texCoords;
} gs_in[];
out vec2 TexCoords;
uniform float time;
vec4 explode(vec4 position, vec3 normal) { ... }
vec3 GetNormal() { ... }
void main() {
vec3 normal = GetNormal();
gl_Position = explode(gl_in[0].gl_Position, normal);
TexCoords = gs_in[0].texCoords;
EmitVertex();
gl_Position = explode(gl_in[1].gl_Position, normal);
TexCoords = gs_in[1].texCoords;
EmitVertex();
gl_Position = explode(gl_in[2].gl_Position, normal);
TexCoords = gs_in[2].texCoords;
EmitVertex();
EndPrimitive();
}Notez que nous produisons aussi des coordonnées de texture appropriées avant d’émettre un sommet.
Aussi, n’oubliez pas de définir la variable time dans le code OpenGL :
shader.setFloat("time", glfwGetTime());Le résultat donne un modèle 3D qui semble exploser continuellement et qui redevient normal. Bien que ce ne soit pas très pratique, cela montre une utilisation un peu plus avancée du geometry shader. Vous pouvez comparer votre code avec celui-ci.
IX-D. Visualiser les normales▲
Dans cette section, nous allons voir comment utiliser le geometry shader pour une chose utile : la visualisation des normales d’un objet. Lorsque vous programmez les shaders pour l’éclairage, vous allez probablement obtenir des résultats étranges. Une source classique pour les problèmes d’éclairage est un mauvais chargement des données des sommets, ce qui provoque une mauvaise définition des normales. Nous voulons donc une méthode pour vérifier que les normales sont correctes. Une bonne façon est de les afficher grâce au geometry shader.
L’idée est la suivante : nous dessinons d’abord la scène, sans geometry shader, puis nous la dessinons une deuxième fois, mais uniquement en affichant les normales générées par le geometry shader. Ce dernier prend en entrée un triangle et génère trois lignes à partir de ceux-ci, dans la direction de la normale : une normale pour chaque sommet. En pseudo-code, cela ressemblera à :
shader.use();
DrawScene();
normalDisplayShader.use();
DrawScene();Cette fois, nous créons un geometry shader qui utilise les normales fournies par le modèle au lieu de les générer nous-mêmes. Pour gérer la mise à l’échelle et les rotations (à cause de la matrice de modèle et de vue), nous allons transformer les normales en premier avec la matrice de normale avant de passer en espace de coordonnées de l’écran (le geometry shader reçoit le vecteur de position dans l’espace de découpage, nous devons donc aussi transformer les normales afin de les avoir dans cet espace de coordonnées). Cela peut se faire dans le vertex shader :
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
out VS_OUT {
vec3 normal;
} vs_out;
uniform mat4 projection;
uniform mat4 view;
uniform mat4 model;
void main()
{
gl_Position = projection * view * model * vec4(aPos, 1.0);
mat3 normalMatrix = mat3(transpose(inverse(view * model)));
vs_out.normal = normalize(vec3(projection * vec4(normalMatrix * aNormal, 0.0)));
}La normale en espace de découpage est ensuite passé à l’étape suivante du pipeline à travers le bloc d’interface. Le geometry shader prend chaque sommet (avec leur position et leur normale) et dessine une normale pour chaque position :
#version 330 core
layout (triangles) in;
layout (line_strip, max_vertices = 6) out;
in VS_OUT {
vec3 normal;
} gs_in[];
const float MAGNITUDE = 0.4;
void GenerateLine(int index)
{
gl_Position = gl_in[index].gl_Position;
EmitVertex();
gl_Position = gl_in[index].gl_Position + vec4(gs_in[index].normal, 0.0) * MAGNITUDE;
EmitVertex();
EndPrimitive();
}
void main()
{
GenerateLine(0); // première normale
GenerateLine(1); // deuxième normale
GenerateLine(2); // troisième normale
}Le contenu du geometry shader doit être explicite. Notez que nous multiplions la normale avec le vecteur MAGNITUDE pour limiter la taille de la normale affichée (sinon, elle serait trop grande).
Comme la visualisation des normales est surtout utilisée pour le débogage, nous pouvons les afficher avec une seule couleur (ou de manière très colorée) avec l’aide du fragment shader :
#version 330 core
out vec4 FragColor;
void main()
{
FragColor = vec4(1.0, 1.0, 0.0, 1.0);
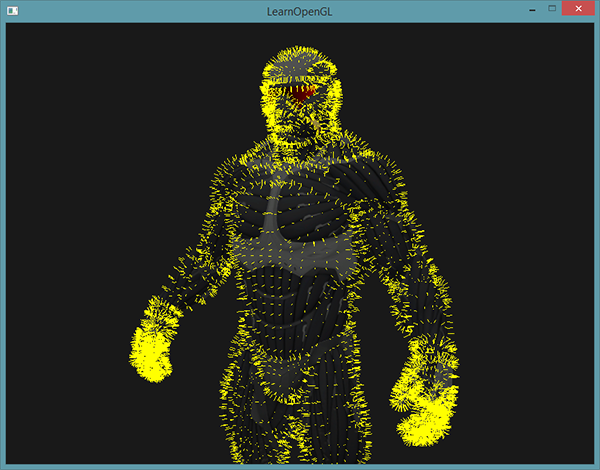
}L’affichage du modèle en deux passes avec le shader spécial de visualisation des normales devrait donner quelque chose comme ça :
Mis à part que la nanosuit ressemble maintenant à un homme chevelu avec des moufles, cela offre une méthode utile pour déterminer si les normales du modèle sont correctes. Vous pouvez imaginer qu’un tel geometry shader est très pratique pour ajouter de la fourrure aux objets.
Vous pouvez trouver le code source OpenGL ici.
IX-E. Remerciements▲
Ce tutoriel est une traduction réalisée par Alexandre Laurent dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.