9. Transformations▲
On sait maintenant comment créer des objets, les colorer ou leur donner une apparence avec une texture, mais cela reste des objets statiques et donc peu intéressants. On pourrait essayer de les faire bouger en modifiant les sommets et en reconfigurant les tampons à chaque rendu, mais ce serait pénible et peu efficace. Il y a mieux à faire pour transformer un objet, en utilisant une (ou plusieurs) matrice de transformation.
Les matrices sont des outils mathématiques puissants qui peuvent effrayer au début, mais qui se révèlent très pratiques et utiles ensuite. Nous allons devoir parler un peu de maths, et pour les lecteurs qui souhaiteraient approfondir le sujet, je conseillerai des lectures additionnelles.
Pour bien comprendre les transformations, il nous faut présenter les vecteurs avant de parler des matrices. Le but de ce chapitre est de vous donner quelques bases de maths sur les sujets qui nous seront nécessaires par la suite. En cas de difficultés, essayez d’en comprendre le plus possible et revenez-y plus tard en cas de besoin.
9-1. Les vecteurs▲
Dans leur définition la plus basique, les vecteurs sont des directions, rien de plus. Un vecteur a une direction et une longueur (appelée aussi norme).
Par exemple, vous pouvez imaginer un vecteur comme une direction sur une carte au trésor : aller 10 pas vers la gauche, puis 3 pas vers le nord, puis 3 pas vers la droite. Ici « gauche » est la première direction, et « 10 pas » est la longueur du premier vecteur. Le chemin vers le trésor est constitué de 3 vecteurs.
Les vecteurs peuvent avoir n’importe quelle dimension, mais nous travaillerons en dimension 2, 3 ou 4. Si un vecteur est de dimension 2, il représente une direction dans un plan (2D) ; de dimension 3 il représente une direction dans l’espace (3D).
Ci-dessous sont représentés trois vecteurs où chacun est figuré avec une flèche et ses coordonnées. Vous pouvez imaginer un vecteur 2D comme un vecteur 3D ayant la coordonnée z = 0. Puisque ce sont des directions, l’origine d’un vecteur ne change pas sa valeur. Ici les vecteurs kitxmlcodeinlinelatexdvp\vec{v}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\vec{w}finkitxmlcodeinlinelatexdvp sont les mêmes, bien qu’ils n’aient pas la même origine :
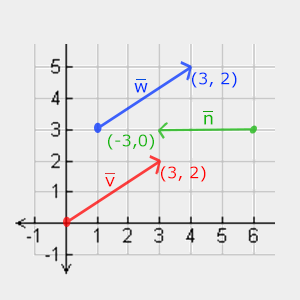
Pour nommer les vecteurs, les mathématiciens utilisent des flèches qu’ils placent au-dessus de la lettre pour bien montrer qu’il s’agit d’un vecteur. Par exemple si x, y, z sont les coordonnées du vecteur kitxmlcodeinlinelatexdvp\vec{v}finkitxmlcodeinlinelatexdvp:
kitxmlcodelatexdvp\vec{v} = \begin{pmatrix} \color{red}x \\ \color{green}y \\ \color{blue}z \end{pmatrix}finkitxmlcodelatexdvpPuisque les vecteurs représentent des directions, il est quelquefois difficile de les visualiser à une certaine position. Ce que l’on fait souvent consiste à les placer avec l’origine en (0, 0, 0) et ensuite de les faire pointer dans la direction représentée, vers un point de coordonnées identiques à celles du vecteur. Le vecteur (3, 2) pointe vers le point (3, 2) si l’on place son origine en (0, 0), comme le vecteur v de la figure précédente. On peut donc utiliser les vecteurs pour décrire une direction, mais aussi une position, en 2D ou en 3D.
Comme avec les nombres, on peut définir plusieurs opérations sur les vecteurs (nous avons déjà rencontré certaines opérations dans les chapitres précédents).
9-2. Opérations entre vecteur et scalaire▲
Un scalaire est un simple nombre. On peut effectuer les quatre opérations (+, -, *, /) entre un vecteur et un scalaire, consistant à faire l’opération donnée avec chacune des composantes de ce vecteur :
Pour l’addition par exemple :
kitxmlcodelatexdvp\begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix} + x = \begin{pmatrix} \color{red}1 + x \\ \color{green}2 + x \\ \color{blue}3 + x \end{pmatrix}finkitxmlcodelatexdvpOn peut utiliser les quatre opérations, mais attention, pour – et /, l’ordre est important, seules la soustraction et la division par un scalaire sont possibles (on ne peut pas diviser un scalaire par un vecteur).
9-3. Négation▲
La négation d’un vecteur consiste à inverser sa direction en changeant de signe chacune de ses composantes (ou coordonnées). Cela revient à le multiplier par -1 :
kitxmlcodelatexdvp-\vec{v} = -\begin{pmatrix} \color{red}{v_x} \\ \color{blue}{v_y} \\ \color{green}{v_z} \end{pmatrix} = \begin{pmatrix} -\color{red}{v_x} \\ -\color{blue}{v_y} \\ -\color{green}{v_z} \end{pmatrix}finkitxmlcodelatexdvp9-4. Addition et soustraction entre vecteurs▲
L’addition de deux vecteurs consiste à additionner leurs composantes respectives :
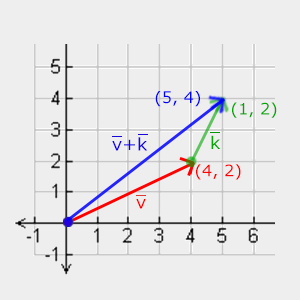
kitxmlcodelatexdvp\vec{v} = \begin{pmatrix} \color{red}1 \\ \color{green}2 \\ \color{blue}3 \end{pmatrix}, \vec{k} = \begin{pmatrix} \color{red}4 \\ \color{green}5 \\ \color{blue}6 \end{pmatrix} \rightarrow \vec{v} + \vec{k} = \begin{pmatrix} \color{red}1 + \color{red}4 \\ \color{green}2 + \color{green}5 \\ \color{blue}3 + \color{blue}6 \end{pmatrix} = \begin{pmatrix} \color{red}5 \\ \color{green}7 \\ \color{blue}9 \end{pmatrix}finkitxmlcodelatexdvpVisuellement, cela se représente comme dans la figure ci-dessous :
kitxmlcodeinlinelatexdvp\vec{v} = (4,2)finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\vec{k} = (1,2)finkitxmlcodeinlinelatexdvp donc kitxmlcodeinlinelatexdvp\vec{v} + \vec{k} = (5,4)finkitxmlcodeinlinelatexdvp
La soustraction suit le même procédé, mais la figure est différente. Le résultat est le vecteur qui va de l’extrémité d’un vecteur à l’extrémité de l’autre :
kitxmlcodelatexdvp(0.5, 3.5) – (3, 2) = (-2.5, 1.5)finkitxmlcodelatexdvp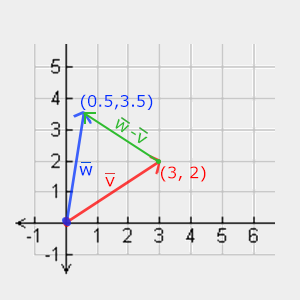
La différence entre deux vecteurs position peut s’avérer très utile pour calculer la direction définie par deux points de l’espace.
9-5. Longueur▲
Pour retrouver la longueur d’un vecteur, on peut utiliser le théorème de Pythagore. Un vecteur de coordonnées (x, y) forme l’hypoténuse d’un triangle rectangle, les deux autres côtés ayant pour longueur x et y :
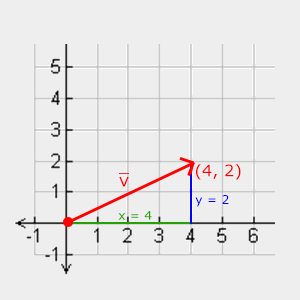
Où kitxmlcodeinlinelatexdvp||\color{red}{\vec{v}}||finkitxmlcodeinlinelatexdvp est la longueur (ou norme) de kitxmlcodeinlinelatexdvp\vec{v}finkitxmlcodeinlinelatexdvp.
Cela s’étend facilement au cas 3D en ajoutant la composante z à la formule.
Dans cet exemple, la longueur du vecteur (4, 2) se calcule ainsi :
kitxmlcodelatexdvp||\color{red}{\vec{v}}|| = \sqrt{\color{green}4^2 + \color{blue}2^2} = \sqrt{\color{green}16 + \color{blue}4} = \sqrt{20} = 4.47finkitxmlcodelatexdvpUn cas particulier de vecteur est le vecteur unitaire : sa longueur est égale à 1. On peut définir un vecteur unitaire dans la même direction que kitxmlcodeinlinelatexdvp\vec{v}finkitxmlcodeinlinelatexdvp, simplement en le divisant par sa longueur. On appelle cela normaliser un vecteur. On utilise souvent ces vecteurs unitaires pour indiquer seulement une direction (la direction d’un vecteur ne change pas si l’on ne modifie que sa longueur).
9-6. Produit de vecteurs▲
Multiplier deux vecteurs peut paraître étrange, mais on peut en fait définir deux opérations appelées l’une produit scalaire noté kitxmlcodeinlinelatexdvp\vec{v} \cdot \vec{k}finkitxmlcodeinlinelatexdvp et l’autre produit vectoriel noté kitxmlcodeinlinelatexdvp\vec{v} \times \vec{k}finkitxmlcodeinlinelatexdvp
9-6-1. Produit scalaire▲
Le produit scalaire de deux vecteurs est égal au produit de leur longueur multiplié par le cosinus de l’angle qu’ils forment entre eux. L’angle étant noté θ, le produit scalaire est :
kitxmlcodelatexdvp\vec{v} \cdot \vec{k} = ||\vec{v}|| \cdot ||\vec{k}|| \cdot \cos \thetafinkitxmlcodelatexdvpCe produit est très utile. Supposons que kitxmlcodeinlinelatexdvp\vec{v}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvp\vec{k}finkitxmlcodeinlinelatexdvp soient deux vecteurs unitaires, le produit scalaire vaut alors simplement cos(θ). Cette valeur vaut 1 si l’angle vaut 0, et vaut 0 si l’angle vaut 90°. Cela permet par exemple de tester si deux vecteurs sont parallèles (0°) ou orthogonaux (90°). Pour en savoir plus sur les fonctions sin et cos, vous pouvez suivre les cours de la Khan Academy sur la trigonométrie.
On peut aussi s’en servir pour calculer l’angle entre deux vecteurs quelconques en divisant le produit scalaire par le produit des longueurs, on obtient alors cos(θ).
Le produit scalaire se calcule simplement en multipliant entre elles les composantes des deux vecteurs et en ajoutant ces produits. Par exemple :
kitxmlcodelatexdvp\begin{pmatrix} \color{red}{0.6} \\ -\color{green}{0.8} \\ \color{blue}0 \end{pmatrix} \cdot \begin{pmatrix} \color{red}0 \\ \color{green}1 \\ \color{blue}0 \end{pmatrix} = (\color{red}{0.6} * \color{red}0) + (-\color{green}{0.8} * \color{green}1) + (\color{blue}0 * \color{blue}0) = -0.8finkitxmlcodelatexdvpPour calculer l’angle, on calcule la longueur de chaque vecteur, qui dans cet exemple valent 1, ce qui signifie que cos(θ) = -0.8 et donc θ = 143 degrés. Le produit scalaire est très utilisé en maths et en physique.
9-6-2. Produit vectoriel▲
Le résultat du produit vectoriel (utilisé en 3D) est un vecteur qui est orthogonal aux deux vecteurs considérés. Si ces deux vecteurs sont orthogonaux, ils formeront avec le vecteur produit un ensemble de trois vecteurs orthogonaux, ce qui nous sera très utile dans la suite.
L’image suivante donne un aperçu du résultat :
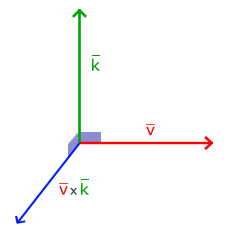
Le calcul des composantes du produit vectoriel n’est pas évident, et pour ne pas alourdir l’exposé, nous donnerons seulement la formule permettant de calculer ce produit vectoriel :
kitxmlcodelatexdvp\begin{pmatrix} \color{red}{A_{x}} \\ \color{green}{A_{y}} \\ \color{blue}{A_{z}} \end{pmatrix} \times \begin{pmatrix} \color{red}{B_{x}} \\ \color{green}{B_{y}} \\ \color{blue}{B_{z}} \end{pmatrix} = \begin{pmatrix} \color{green}{A_{y}} \cdot \color{blue}{B_{z}} - \color{blue}{A_{z}} \cdot \color{green}{B_{y}} \\ \color{blue}{A_{z}} \cdot \color{red}{B_{x}} - \color{red}{A_{x}} \cdot \color{blue}{B_{z}} \\ \color{red}{A_{x}} \cdot \color{green}{B_{y}} - \color{green}{A_{y}} \cdot \color{red}{B_{x}} \end{pmatrix}finkitxmlcodelatexdvpCette formule n’est pas très parlante, il faut surtout retenir que le résultat donne un vecteur orthogonal aux deux autres (si les deux vecteurs ne sont pas colinéaires, car dans ce cas, le produit vectoriel est le vecteur nul).
9-7. Matrices▲
Nous avons présenté rapidement les vecteurs, voyons maintenant les matrices. Une matrice est basiquement un tableau rectangulaire de nombres. Chaque nombre est appelé élément de la matrice, voici un exemple de matrice 2x3 (2 lignes et 3 colonnes, ce sont les dimensions de la matrice) :
kitxmlcodelatexdvp\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}finkitxmlcodelatexdvpLes éléments sont repérés par l’indice de leur colonne et de leur ligne, on attribue l’indice 0 à la première ligne (en haut) et à la première colonne (à gauche). Dans cet exemple, M[1, 0] = 4.
Les matrices ne sont rien de plus que des tableaux de nombres, mais possèdent des propriétés mathématiques très utiles. On peut définir certaines opérations sur les matrices, parmi lesquelles l’addition, la soustraction et la multiplication.
9-7-1. Addition et soustraction▲
On peut ajouter un nombre (scalaire) à une matrice en ajoutant ce nombre à chacun des éléments de la matrice :
kitxmlcodelatexdvp\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \color{green}3 = \begin{bmatrix} 1 + \color{green}3 & 2 + \color{green}3 \\ 3 + \color{green}3 & 4 + \color{green}3 \end{bmatrix} = \begin{bmatrix} 4 & 5 \\ 6 & 7 \end{bmatrix}finkitxmlcodelatexdvpIdem pour la soustraction :
kitxmlcodelatexdvp\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} - \color{green}3 = \begin{bmatrix} 1 - \color{green}3 & 2 - \color{green}3 \\ 3 - \color{green}3 & 4 - \color{green}3 \end{bmatrix} = \begin{bmatrix} -2 & -1 \\ 0 & 1 \end{bmatrix}finkitxmlcodelatexdvpL’addition et la soustraction entre matrices se fait élément par élément. Ces opérations n’étant possibles que pour deux matrices de mêmes dimensions :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} + \begin{bmatrix} \color{red}5 & \color{red}6 \\ \color{green}7 & \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 + \color{red}5 & \color{red}2 + \color{red}6 \\ \color{green}3 + \color{green}7 & \color{green}4 + \color{green}8 \end{bmatrix} = \begin{bmatrix} \color{red}6 & \color{red}8 \\ \color{green}{10} & \color{green}{12} \end{bmatrix}finkitxmlcodelatexdvpLe calcul est identique pour une soustraction :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}4 & \color{red}2 \\ \color{green}1 & \color{green}6 \end{bmatrix} - \begin{bmatrix} \color{red}2 & \color{red}4 \\ \color{green}0 & \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}4 - \color{red}2 & \color{red}2 - \color{red}4 \\ \color{green}1 - \color{green}0 & \color{green}6 - \color{green}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & -\color{red}2 \\ \color{green}1 & \color{green}5 \end{bmatrix}finkitxmlcodelatexdvp9-7-2. Produit par un scalaire▲
Dans ce cas, on multiplie chaque élément de la matrice par le scalaire :
kitxmlcodelatexdvp\color{green}2 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} \color{green}2 \cdot 1 & \color{green}2 \cdot 2 \\ \color{green}2 \cdot 3 & \color{green}2 \cdot 4 \end{bmatrix} = \begin{bmatrix} 2 & 4 \\ 6 & 8 \end{bmatrix}finkitxmlcodelatexdvpOn peut noter que cette opération est en réalité une mise à l’échelle (ici une multiplication par 2), d’où l’origine du mot « scalaire » (scale en anglais).
9-7-3. Multiplication de deux matrices▲
Cette opération n’est pas très complexe mais peut apparaître comme peu évidente. On multiplie les éléments entre eux selon certaines règles. Cette opération exige cependant une condition sur leurs dimensions : on ne peut multiplier deux matrices que si le nombre de colonnes de la matrice de gauche est égal au nombre de lignes de la matrice de droite.
Attention : contrairement aux nombres, l’ordre de la multiplication est important : kitxmlcodeinlinelatexdvpA \cdot B \neq B \cdot Afinkitxmlcodeinlinelatexdvp (opération non commutative).
Prenons un exemple avec deux matrices 2x2 :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}1 & \color{red}2 \\ \color{green}3 & \color{green}4 \end{bmatrix} \cdot \begin{bmatrix} \color{blue}5 & \color{purple}6 \\ \color{blue}7 & \color{purple}8 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot \color{blue}5 + \color{red}2 \cdot \color{blue}7 & \color{red}1 \cdot \color{purple}6 + \color{red}2 \cdot \color{purple}8 \\ \color{green}3 \cdot \color{blue}5 + \color{green}4 \cdot \color{blue}7 & \color{green}3 \cdot \color{purple}6 + \color{green}4 \cdot \color{purple}8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}finkitxmlcodelatexdvpLes éléments de la matrice produit sont le résultat du produit d’une ligne de la matrice de gauche par une colonne de la matrice de droite, comme le montrent les couleurs employées dans la figure :
Pour calculer le premier élément, d’indices (0,0), on utilise la première ligne de la matrice de gauche et la première colonne de la matrice de droite, en multipliant chacun des éléments deux à deux et en effectuant la somme de ces produits. On répète cette opération pour chacun des éléments de la matrice produit. Pour calculer l’élément de la ligne i et de la colonne j, on utilise la ligne i de la matrice de gauche et la colonne j de la matrice de droite.
La matrice produit est une matrice de dimensions (n,m), n étant le nombre de lignes de la matrice de gauche et m le nombre de colonnes de la matrice de droite.
Ne vous inquiétez pas si vous avez quelques difficultés avec ces calculs, essayez juste de les réaliser tranquillement à la main et revenez sur cette page en cas de difficultés. La multiplication des matrices vous deviendra vite familière.
Voici un autre exemple, plus compliqué, avec des matrices 3x3. Essayez de faire les calculs vous-mêmes et comparez vos résultats pour vous habituer à ces calculs :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}4 & \color{red}2 & \color{red}0 \\ \color{green}0 & \color{green}8 & \color{green}1 \\ \color{blue}0 & \color{blue}1 & \color{blue}0 \end{bmatrix} \cdot \begin{bmatrix} \color{red}4 & \color{green}2 & \color{blue}1 \\ \color{red}2 & \color{green}0 & \color{blue}4 \\ \color{red}9 & \color{green}4 & \color{blue}2 \end{bmatrix} = \begin{bmatrix} \color{red}4 \cdot \color{red}4 + \color{red}2 \cdot \color{red}2 + \color{red}0 \cdot \color{red}9 & \color{red}4 \cdot \color{green}2 + \color{red}2 \cdot \color{green}0 + \color{red}0 \cdot \color{green}4 & \color{red}4 \cdot \color{blue}1 + \color{red}2 \cdot \color{blue}4 + \color{red}0 \cdot \color{blue}2 \\ \color{green}0 \cdot \color{red}4 + \color{green}8 \cdot \color{red}2 + \color{green}1 \cdot \color{red}9 & \color{green}0 \cdot \color{green}2 + \color{green}8 \cdot \color{green}0 + \color{green}1 \cdot \color{green}4 & \color{green}0 \cdot \color{blue}1 + \color{green}8 \cdot \color{blue}4 + \color{green}1 \cdot \color{blue}2 \\ \color{blue}0 \cdot \color{red}4 + \color{blue}1 \cdot \color{red}2 + \color{blue}0 \cdot \color{red}9 & \color{blue}0 \cdot \color{green}2 + \color{blue}1 \cdot \color{green}0 + \color{blue}0 \cdot \color{green}4 & \color{blue}0 \cdot \color{blue}1 + \color{blue}1 \cdot \color{blue}4 + \color{blue}0 \cdot \color{blue}2 \end{bmatrix} \\ = \begin{bmatrix} 20 & 8 & 12 \\ 25 & 4 & 34 \\ 2 & 0 & 4 \end{bmatrix}finkitxmlcodelatexdvpPas d’inquiétude si cela ne vous semble pas simple, il faut surtout savoir à quoi servent ces multiplications de matrices. D’autre part, les bibliothèques mathématiques effectuent ces calculs pour nous. Pour une présentation plus détaillée, voir les vidéos de la Khan Academy à propos des matrices.
9-8. Multiplication d’un vecteur par une matrice▲
Nous avons déjà utilisé les vecteurs pour représenter des positions, des couleurs et aussi des coordonnées de textures. On peut aussi considérer les vecteurs comme des matrices Nx1, où N est la dimension (3 en 3D), soit des matrices à 1 seule colonne. On peut donc multiplier une matrice par un vecteur de dimension N à condition que cette matrice possède N colonnes.
Mais quel est l’intérêt de cette multiplication ? En fait, nous allons pouvoir transformer notre vecteur au moyen d’une (ou plusieurs) matrices. Voyons ces possibilités en détail.
9-9. La matrice identité▲
Dans OpenGL, on utilise en général des matrices 4x4 pour plusieurs raisons, mais essentiellement, car les vecteurs ont généralement quatre composantes. La matrice la plus simple que l’on peut concevoir est la matrice identité, où tous les éléments sont nuls sauf ceux de la première diagonale où tous les éléments valent 1. Si l’on multiplie un vecteur par cette matrice, on laisse le vecteur inchangé :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix} = \begin{bmatrix} \color{red}1 \cdot 1 \\ \color{green}1 \cdot 2 \\ \color{blue}1 \cdot 3 \\ \color{purple}1 \cdot 4 \end{bmatrix} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 4 \end{bmatrix}finkitxmlcodelatexdvpLe vecteur n’est pas modifié, ce qui devient clair lorsque l’on applique les règles de la multiplication. Pour le premier élément, le calcul est le suivant :
kitxmlcodelatexdvp\color{red}1\cdot1 + \color{red}0\cdot2 + \color{red}0\cdot3 + \color{red}0\cdot4 = 1finkitxmlcodelatexdvpet il en est de même pour les autres éléments.
Mais pourquoi utiliser une matrice qui ne modifie pas le vecteur sur lequel elle opère ? En fait, cette matrice identité est souvent un point de départ pour générer d’autres matrices de transformation, et elle joue un rôle fondamental en algèbre linéaire.
9-10. Matrice de mise à l’échelle d’un vecteur▲
Mettre un vecteur à une autre échelle consiste à modifier sa longueur sans modifier sa direction, en multipliant le vecteur par un scalaire (voir 8.2). Mais puisque l’on travaille en 2D ou en 3D, on peut utiliser une échelle différente pour chacune des dimensions, et utiliser un scalaire par dimension.
Par exemple, considérons le vecteur kitxmlcodeinlinelatexdvp\vec{v} = (3, 2)finkitxmlcodeinlinelatexdvp. Nous pouvons choisir une mise à l’échelle de 0.5 en x et 2 en y, ce qui le rendra deux fois moins large et deux fois plus haut, pour donner le vecteur kitxmlcodeinlinelatexdvp\vec{s} = (0.5, 2)finkitxmlcodeinlinelatexdvp :
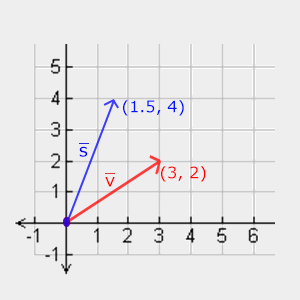
Rappelons-nous qu’OpenGL opère en général en 3D, et donc pour un cas 2D il suffit d’utiliser l’échelle 1 pour la coordonnée z. Si l’on utilise le même scalaire pour chaque dimension, on parle alors de mise à l’échelle uniforme.
Construisons une matrice pour réaliser cette opération. En changeant les valeurs 1 de la matrice identité par les scalaires choisis pour la mise à l’échelle, on réalisera cette mise à l’échelle en multipliant le vecteur par la matrice. Si les facteurs d’échelle sont définis par les variables kitxmlcodeinlinelatexdvp(\color{red}{S_1}, \color{green}{S_2}, \color{blue}{S_3})finkitxmlcodeinlinelatexdvp, on peut composer la matrice de mise à l’échelle avec ces valeurs et l’opération de mise à l’échelle sera ainsi définie pour tout vecteur (x, y, z) :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}{S_1} & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{S_2} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}{S_3} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{S_1} \cdot x \\ \color{green}{S_2} \cdot y \\ \color{blue}{S_3} \cdot z \\ 1 \end{pmatrix}finkitxmlcodelatexdvpNotons que la 4e valeur est fixée à 1, car nous ne modifions pas la composante w du vecteur 3D. On utilise w pour d’autres raisons que nous allons examiner dans la suite.
9-11. Matrice de translation d’un vecteur position▲
Cette opération consiste à ajouter un autre vecteur au vecteur considéré pour obtenir une nouvelle position. Nous avons déjà rencontré l’addition de vecteurs, cela ne devrait pas vous paraître nouveau.
De la même façon que pour la mise à l’échelle, nous pouvons utiliser une matrice 4x4 pour réaliser cette opération d’addition. Dans ce cas, nous utilisons les trois premières valeurs de la 4e colonne.
Soient kitxmlcodeinlinelatexdvp(\color{red}{T_x},\color{green}{T_y},\color{blue}{T_z})finkitxmlcodeinlinelatexdvples composantes du vecteur de translation, l’opération de translation se déroulera ainsi :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}{T_x} \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}{T_y} \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}{T_z} \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + \color{red}{T_x} \\ y + \color{green}{T_y} \\ z + \color{blue}{T_z} \\ 1 \end{pmatrix}finkitxmlcodelatexdvpCela fonctionne car la composante w du vecteur est égale à 1, le calcul de la première valeur se déroulant ainsi : 1.x + 0.y + 0.z + Tx.1 = x + Tx.
On voit l’intérêt de travailler en dimension 4, cette opération n’aurait pas été possible avec une matrice 3x3.
Coordonnées homogènes
La composante w est appelée coordonnée homogène. Pour obtenir le vecteur 3D à partir d’un vecteur homogène, on divise x, y et z par w. La plupart du temps, w = 1.0 et cela ne change rien. L’utilisation de coordonnées homogènes présente plusieurs avantages ; elles permettent d’effectuer des translations sur les vecteurs 3D et nous les utiliserons aussi pour créer des effets visuels dans le prochain chapitre.
Si la coordonnée w vaut 0, le vecteur est appelé vecteur de direction, on ne peut pas le translater.
Avec les matrices de translation, on peut simplement déplacer des objets dans l’espace, cette opération se révèle très utile dans les applications 3D.
9-12. Matrice de rotation d’un vecteur▲
Les rotations sont plus difficiles à comprendre. Pour une présentation détaillée, on pourra consulter les vidéos de la Khan Academy sur l'algèbre linéaire.
La rotation d’un vecteur consiste à le faire tourner. Une rotation est définie par son axe (autour duquel tourne le vecteur) et l’angle de rotation. Un angle peut être mesuré en radians ou en degrés (un tour entier vaut 360° ou 2.Pi radians). Pour passer d’une mesure à l’autre :
La plupart des fonctions de rotation utilisent des angles définis en radians, mais on passe facilement d’un système à l’autre :
angle en degrés = angle en radians * (180.0f / PI)
angle en radians = angle en degrés * (PI / 180.0f)Une rotation d’un demi-tour correspond à un angle de 180° (360/2), et une rotation de 1/5e de tour correspond à un angle de 72° (360/5).
Un exemple de rotation en 2D est montré dans la figure ci-dessous, le vecteur kitxmlcodeinlinelatexdvp\vec{v}finkitxmlcodeinlinelatexdvp tourne de 72° autour de l’axe z (dirigé vers nous) pour donner le vecteur kitxmlcodeinlinelatexdvp\vec{k}finkitxmlcodeinlinelatexdvp.
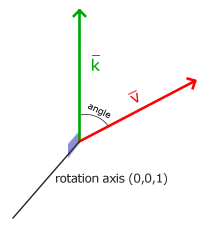
Les rotations en 3D requièrent de définir un angle mais aussi un axe de rotation. Essayez de visualiser cela en tournant votre tête d’un certain angle vers la droite ou la gauche tout en fixant votre regard vers le bas. Lorsque l’on fait tourner des vecteurs en 2D, l’axe de rotation est l’axe z (essayez de la visualiser).
En utilisant la trigonométrie, il est possible de transformer un vecteur par une rotation d’un angle donné, en utilisant les fonctions sinus et cosinus. Le calcul de ces matrices dépasse le cadre de ce tutoriel. Les matrices de rotation autour des axes x, y et z sont assez simples (θ est l’angle de rotation) :
Rotation autour de l’axe X :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}{\cos \theta} & - \color{green}{\sin \theta} & \color{green}0 \\ \color{blue}0 & \color{blue}{\sin \theta} & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ \color{green}{\cos \theta} \cdot y - \color{green}{\sin \theta} \cdot z \\ \color{blue}{\sin \theta} \cdot y + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}finkitxmlcodelatexdvpRotation autour de l’axe Y :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}{\cos \theta} & \color{red}0 & \color{red}{\sin \theta} & \color{red}0 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}0 \\ - \color{blue}{\sin \theta} & \color{blue}0 & \color{blue}{\cos \theta} & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x + \color{red}{\sin \theta} \cdot z \\ y \\ - \color{blue}{\sin \theta} \cdot x + \color{blue}{\cos \theta} \cdot z \\ 1 \end{pmatrix}finkitxmlcodelatexdvpRotation autour de l’axe Z :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}{\cos \theta} & - \color{red}{\sin \theta} & \color{red}0 & \color{red}0 \\ \color{green}{\sin \theta} & \color{green}{\cos \theta} & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} \cdot \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} \color{red}{\cos \theta} \cdot x - \color{red}{\sin \theta} \cdot y \\ \color{green}{\sin \theta} \cdot x + \color{green}{\cos \theta} \cdot y \\ z \\ 1 \end{pmatrix}finkitxmlcodelatexdvpEn utilisant ces matrices, on peut faire tourner un vecteur autour de l’un des trois axes X, Y et Z. On peut aussi les combiner avec plusieurs rotations successives, autour de l’axe X puis de l’axe Y par exemple. Cela introduit par contre le problème du Gimbal lock. Nous ne discuterons pas ce point délicat, mais une meilleure solution consiste à définir directement une rotation autour d’un axe quelconque, par exemple (0.662, 0.2, 0.722) – notons que l’axe est défini par un vecteur unitaire – au moyen d’une matrice de rotation. Si l’axe de rotation est défini par ses composantes
kitxmlcodeinlinelatexdvp(\color{red}{R_x}, \color{green}{R_y}, \color{blue}{R_z})finkitxmlcodeinlinelatexdvp, la matrice de rotation d’un angle θ autour de cet axe sera la suivante :
kitxmlcodelatexdvp\begin{bmatrix} \cos \theta + \color{red}{R_x}^2(1 - \cos \theta) & \color{red}{R_x}\color{green}{R_y}(1 - \cos \theta) - \color{blue}{R_z} \sin \theta & \color{red}{R_x}\color{blue}{R_z}(1 - \cos \theta) + \color{green}{R_y} \sin \theta & 0 \\ \color{green}{R_y}\color{red}{R_x} (1 - \cos \theta) + \color{blue}{R_z} \sin \theta & \cos \theta + \color{green}{R_y}^2(1 - \cos \theta) & \color{green}{R_y}\color{blue}{R_z}(1 - \cos \theta) - \color{red}{R_x} \sin \theta & 0 \\ \color{blue}{R_z}\color{red}{R_x}(1 - \cos \theta) - \color{green}{R_y} \sin \theta & \color{blue}{R_z}\color{green}{R_y}(1 - \cos \theta) + \color{red}{R_x} \sin \theta & \cos \theta + \color{blue}{R_z}^2(1 - \cos \theta) & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}finkitxmlcodelatexdvpLa démonstration est hors de propos ici. Cependant, cette matrice ne résout pas complètement le problème du gimbal lock. Le mieux est d’utiliser les quaternions, cela est plus sain, et plus facile à calculer. Nous réservons cela pour un autre tutoriel.
9-13. Combiner les matrices▲
La puissance des matrices réside aussi dans la possibilité de combiner plusieurs transformations en une seule matrice grâce à la multiplication des matrices. Voyons cela sur un exemple. Supposons que l’on souhaite mettre à l’échelle 2 un vecteur (x, y, z) et ensuite le translater au moyen du vecteur (1, 2, 3). Nous définissons une matrice de translation et une matrice de mise à l’échelle et nous les multiplions :
kitxmlcodelatexdvpTrans . Scale = \begin{bmatrix} \color{red}1 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}1 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}1 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}0 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}0 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}0 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} = \begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix}finkitxmlcodelatexdvpNoter que nous effectuons la multiplication dans un ordre précis : la translation puis le redimensionnement. La première opération qui sera effectuée sur le vecteur sera la mise à l’échelle, et ensuite la translation. On doit lire la multiplication des matrices de droite à gauche ! Il est conseillé d’effectuer d’abord les mises à l’échelle, puis les rotations et enfin les translations.
L’opération globale sur le vecteur donnera :
kitxmlcodelatexdvp\begin{bmatrix} \color{red}2 & \color{red}0 & \color{red}0 & \color{red}1 \\ \color{green}0 & \color{green}2 & \color{green}0 & \color{green}2 \\ \color{blue}0 & \color{blue}0 & \color{blue}2 & \color{blue}3 \\ \color{purple}0 & \color{purple}0 & \color{purple}0 & \color{purple}1 \end{bmatrix} . \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \color{red}2x + \color{red}1 \\ \color{green}2y + \color{green}2 \\ \color{blue}2z + \color{blue}3 \\ 1 \end{bmatrix}finkitxmlcodelatexdvpVoilà ! Le vecteur obtenu est d’abord mis à l’échelle, puis translaté. Si l’on inverse la multiplication, vous pourrez vérifier que l’on trouverait 2(x+1) = 2x + 2 au lieu de 2x+1…
9-14. En pratique▲
Maintenant que nous avons expliqué les transformations en théorie, il est temps de voir comment utiliser ces connaissances. OpenGL n’offre pas d’objets vecteurs ou matrices, nous devons donc définir nous-mêmes ces objets mathématiques au moyen de classes et de fonctions. Nous ne réaliserons pas cette tâche dans ces tutoriels, nous ferons plutôt appel à des bibliothèques mathématiques. L’une d’entre elles est très adaptée à OpenGL, il s’agit de GLM.
9-15. GLM▲

GLM est l’acronyme de OpenGL Mathematics, qui est une bibliothèque formée uniquement de fichiers d’en-têtes. Il suffira donc d’inclure ces fichiers d’en-têtes pour l’utiliser. Pas besoin de construire cette bibliothèque. GLM peut être téléchargée sur ce site (version 0.9.8). Copiez le contenu du répertoire principal des fichiers d’en-têtes dans votre propre répertoire include et c’est tout.
Depuis la version 0.9.9, GLM initialise par défaut les matrices à 0, au lieu de les initialiser à la matrice identité. Depuis cette version, il est préférable d’initialiser les matrices de cette façon : glm::mat4; mat = glm::mat4(1.0f); Pour utiliser le code de nos tutoriels sans modifications, utilisez une version antérieure à 0.9.9, ou bien initialisez toutes les matrices par la matrice identité.
La plupart des fonctionnalités de GLM se trouvent dans seulement trois fichiers d’en-têtes que nous pouvons inclure comme ceci :
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>Voyons si nous pouvons utiliser nos connaissances pour translater le vecteur (1, 0, 0) au moyen du vecteur (1, 1, 0). Notons que nous définissons notre vecteur avec le type glm::vec4, et la coordonnée w égale à 1.0f.
glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;Nous commençons par définir un vecteur de nom vec, en utilisant la classe vector définie dans GLM. Ensuite nous définissons une matrice 4x4 au moyen du type mat4, initialisée à la matrice identité (attention : pour les versions récentes de GLM, utiliser glm::mat4 trans(1.0);). L’étape suivante consiste à créer une matrice de transformation à partir de la matrice identité, ce qui est réalisé par la fonction glm::translate dont le second paramètre est le vecteur de translation. Ensuite, nous utilisons cette matrice de translation qui ainsi opère sur notre vecteur vec, cela au moyen d’une multiplication. Le vecteur résultant devrait avoir comme coordonnées (1+1, 0+1, 0+0), soit (2, 1, 0), ce que l’on vérifiera aisément.
Effectuons maintenant une mise à l’échelle et une rotation de l’objet conteneur du tutoriel précédent :
glm::mat4 trans;
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));Nous commençons par une mise à l’échelle uniforme d’un facteur 0.5, puis nous effectuons une rotation de 90° autour de l’axe Z. GLM utilise des angles définis en radians, nous convertissons donc les degrés en radians au moyen de la fonction radians(). Notons que le rectangle texturé est dans le plan XY, et que l’axe de rotation est l’axe Z. Nous avons passé la matrice trans en argument de chacune des deux fonctions, le résultat sera donc le produit des deux matrices, combinant ainsi les deux transformations.
La question qui se pose alors : comment passer notre matrice de transformation au shader ? Nous avons vu que le GLSL possède un type mat4. Nous allons donc adapter le vertex shader en y intégrant une variable uniforme de type mat4 et multiplier le vecteur position par cette matrice :
#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;
out vec2 TexCoord;
uniform mat4 transform;
void main()
{
gl_Position = transform * vec4(aPos, 1.0f);
TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}GLSL dispose aussi des types mat2 et mat3 qui permettent des opérations de transformation comme pour les vecteurs. Toutes les opérations que nous avons vues (comme la multiplication d’une matrice par un scalaire, d’un vecteur par une matrice, ou de deux matrices) sont permises sur ces types matrices. Lorsque des opérations particulières sur les matrices se présenteront, nous les expliquerons en détail.
Nous avons ajouté une variable uniforme et multiplié le vecteur position par cette matrice de transformation avant de l’affecter à la variable gl_Position. Notre conteneur devrait être deux fois plus petit et avoir tourné de 90° vers la gauche. Mais il nous reste à passer la matrice de transformation au shader :
unsigned int transformLoc = glGetUniformLocation(ourShader.ID, "transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));Nous récupérons d’abord l’emplacement de la variable uniforme et transmettons ensuite la matrice au shader au moyen de la fonction glUniform munie du suffixe Matrix4fv. Le premier argument désigne l’emplacement de la variable uniforme, le second argument précise combien de matrices nous transmettons (une seule dans notre cas), le troisième argument permet de transposer la matrice, c’est-à-dire inverser lignes et colonnes. Les développeurs OpenGL utilisent souvent une configuration des matrices dans laquelle le premier indice désigne la colonne et le second la ligne, convention aussi utilisée par GLM, il n’est donc pas nécessaire de transposer les matrices, nous laissons cet argument à GL_FALSE. Le dernier paramètre contient la matrice elle-même, mais GLM ne mémorise pas les matrices exactement de la même façon qu’OpenGL souhaite les obtenir, ce qui impose d’utiliser la fonction value_ptr() de GLM.
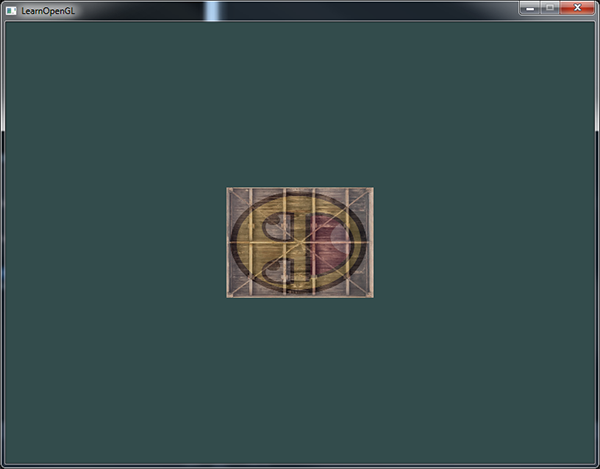
Nous avons créé une matrice de transformation, déclaré une variable uniforme dans le vertex shader et transmis la matrice au shader dans lequel nous transformons nos coordonnées de sommets. Le résultat devrait ressembler à cela :
Parfait ! Notre conteneur est bien tourné vers la gauche et deux fois plus petit qu’avant, la transformation a réussi. Amusons-nous un peu et faisons tourner ce conteneur continuellement, tout en le repositionnant en bas à droite de la fenêtre. Pour qu’il tourne en continu, nous devons mettre à jour la matrice de transformation dans la boucle de rendu, afin de modifier l’angle de rotation constamment. Nous utilisons la fonction glfwGetTime() de GLFW à cet effet :
glm::mat4 trans;
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(), glm::vec3(0.0f, 0.0f, 1.0f));Gardez à l’esprit que dans le cas précédent nous pouvions déclarer la matrice de transformation n’importe où, alors que maintenant, nous devons la recalculer à chaque itération de la boucle de rendu. Lorsque l’on affiche des scènes, il faut en général recalculer les matrices de transformation à chaque passage dans la boucle de rendu pour obtenir un effet de mouvement continu.
Ici, nous commençons par faire tourner le conteneur autour de l’origine (0, 0, 0), et ensuite nous le déplaçons en bas à droite de la fenêtre d’affichage. Rappelez-vous que l’ordre des transformations doit être lu dans l’ordre inverse : même si dans le code nous commençons par la translation et ensuite la rotation, la rotation sera bien effectuée en premier. Comprendre ces transformations et comment elles modifient les objets est assez difficile. Essayez différentes combinaisons de ces transformations et vous comprendrez mieux.
Si vous avez fait les choses correctement, voilà ce que vous obtiendrez :
Un conteneur qui tourne régulièrement, simplement avec une matrice ! Vous voyez maintenant la puissance offerte par les matrices et pourquoi elles sont si utiles dans les applications graphiques. On peut définir une infinité de transformations et les combiner en une seule matrice que l’on peut réutiliser à loisir. Utiliser ces transformations dans le vertex shader nous évite de redéfinir les données des sommets et économise aussi du temps de calcul puisque nous n’avons pas besoin de transmettre les données à chaque fois (ce qui serait assez lent).
Si vous rencontrez quelques problèmes, consultez le code source ainsi que la nouvelle classe shader.
Dans le tutoriel suivant, nous verrons comment utiliser ces matrices pour définir différents espaces de coordonnées pour nos sommets. Ce sera nos premiers pas dans l’univers du graphisme temps réel 3D !
9-16. Lectures▲
- Essence of Linear Algebra : excellente vidéo de Grant Sanderson sur les mathématiques des transformations et de l’algèbre linéaire.
9-17. Exercices▲
- En utilisant la dernière transformation du conteneur, essayez de changer l’ordre des transformations. Voyez ce qui se passe et essayez de comprendre : solution.
- Essayez d’afficher un second conteneur avec un autre appel à glDrawElements() mais placez-le à un endroit différent en utilisant seulement les transformations. Assurez-vous de le placer en haut à gauche de la fenêtre et au lieu de le faire tourner, modifiez sa taille en fonction du temps (la fonction sinus peut s’avérer utile ici, notez aussi que les valeurs négatives de la fonction sinus vont inverser l’objet) : solution.
9-18. Remerciements▲
Ce tutoriel est une traduction réalisée par Jean-Michel Fray dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.