10. Systèmes de Coordonnées▲
Dans le tutoriel précédent, nous avons vu comment utiliser les matrices pour transformer tous les sommets au moyen de matrices de transformation. OpenGL requiert que tous les sommets que nous voulons voir à l'écran soient définis en coordonnées normalisées, c'est-à-dire dans l’intervalle [-1.0, 1.0]. Ce que l’on fait habituellement est de définir les coordonnées dans le système de notre choix, puis de normaliser ces valeurs dans le vertex shader. Ces coordonnées normalisées (NDC) sont ensuite transformées en coordonnées de pixels sur l’écran par le rasterizer.
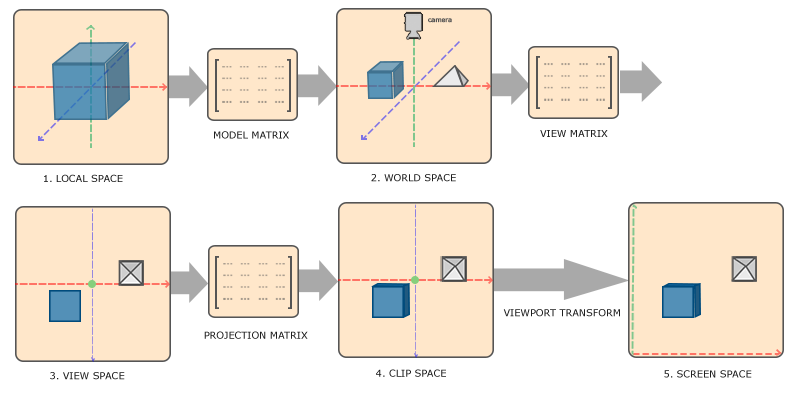
La transformation des coordonnées se fait par étapes. Les coordonnées intermédiaires rendent certaines opérations plus faciles comme nous allons le voir. Nous trouverons ainsi cinq systèmes de coordonnées :
- espace local (ou espace objet) ;
- espace monde (world space) ;
- espace de vue (view space ou eye space) ;
- espace de clip (clip space) ;
- espace écran (screen space).
Ces différents espaces représentent les états successifs dans lesquels seront convertis nos sommets avant de devenir des fragments.
Explicitons cela avec un schéma de chaque étape.
10-1. Le schéma global▲
Pour passer d’un système de coordonnées au suivant, nous utiliserons des matrices de transformation. Les plus importantes sont les matrices de modèle, de vue et de projection. Les coordonnées des sommets sont d’abord exprimées dans l’espace local, puis transformées en coordonnées monde, puis de vue, puis de clip, et enfin d’écran, comme le montre la figure suivante :
- Les coordonnées locales sont les coordonnées de votre objet, relatives à son origine.
- L’étape suivante consiste à les transformer en coordonnées monde, qui sont relatives à un espace plus grand. Elles sont relatives à une origine globale à la scène et qui est partagée par tous les autres objets.
- Ensuite, on transforme ces coordonnées monde en coordonnées de l’espace de vue de telle façon que chaque coordonnée soit comme elle serait si elles étaient vues par la camera, soit le point de vue du spectateur.
- Ensuite, les coordonnées sont projetées sur l’espace de clipping, on ne conserve que les coordonnées dans l’intervalle [0, 1].
- Enfin, on transforme ces valeurs en coordonnées écran par la transformation de la zone de dessin (viewport), dans l’intervalle défini par glViewPort(). Les coordonnées résultantes sont enfin envoyées au rasterizer pour en obtenir des fragments.
Certaines opérations sont plus faciles à réaliser selon l’espace de coordonnées utilisé. Par exemple, la modification d'un objet est plus simple dans l’espace local, tandis que le calcul de la position d’un objet par rapport à d’autres objets est plus simple dans l’espace monde. Cela autorise plus de flexibilité. Voyons ces différents espaces plus en détail.
10-2. L’espace local▲
C’est l’espace dans lequel est défini votre objet. Imaginons que nous créons un cube dans un logiciel de modélisation (comme Blender). L’origine du cube sera sans doute (0, 0, 0), même si le cube doit se trouver finalement à une autre position. Tous les sommets du cube seront définis par rapport à cette origine, ces coordonnées sont locales à l’objet.
Les coordonnées de notre container ont toutes été spécifiées entre -0.5 et 0.5, avec (0, 0) comme origine, ce sont des coordonnées locales.
10-3. Espace monde▲
Si l’on importait tous les objets directement dans l’application, ils seraient sans doute empilés les uns sur les autres au point (0, 0, 0), ce qui n’est pas souhaité ; nous voulons définir leur place dans l’espace monde, les objets étant ainsi répartis dans la scène à leur place respective. Cela est accompli par la transformation définie par la matrice du modèle.
La matrice du modèle translate, diminue ou agrandit et/ou fait tourner les objets pour les placer dans la scène. La matrice utilisée dans le tutoriel précédent pour placer le container est une sorte de matrice de modèle.
10-4. Espace de vue▲
L’espace de vue est ce qu’on appelle la caméra d’OpenGL (appelé encore l’espace de vue ou l’espace caméra). Les coordonnées de l’espace monde sont transformées en fonction de l’emplacement d’où est vue la scène. On obtient ces coordonnées par un ensemble de translations et rotations définies par la matrice de vue. Nous verrons comment définir une telle matrice dans le tutoriel suivant.
10-5. L’espace de clipping▲
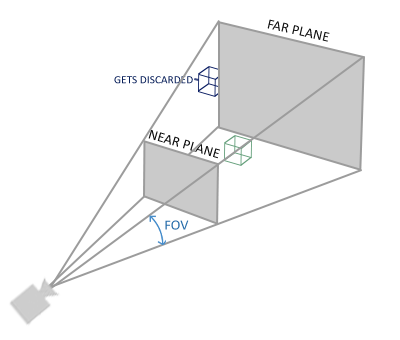
Pour terminer chaque passage du vertex shader, OpenGL attend les coordonnées dans un intervalle spécifique. Les coordonnées en dehors de cet intervalle sont clippées, c'est-à-dire écartées de la scène, ces points ne seront pas visibles. Il est plus simple d’utiliser nos propres coordonnées, puis de les transformer en coordonnées normalisées.
Pour transformer les coordonnées de la vue vers l’espace de clipping, nous définirons une matrice de projection qui spécifie un intervalle de coordonnées, par exemple [-1000, 1000] pour chacune des trois dimensions. La matrice de projection transforme les coordonnées de cet intervalle spécifique en coordonnées normalisées. Les coordonnées en dehors de cet intervalle spécifique ne seront pas projetées sur [-1, +1] et seront donc écartées. Par exemple un sommet en (1250, 500, 750) ne sera pas visible puisque x > 1000.
Si une partie d’une primitive (par exemple un triangle) est en dehors de l’intervalle, OpenGL reconstruit le triangle en un ou plusieurs triangles pour coller à l’espace de clipping.
Cette boîte de vue que crée la matrice de projection est appelée le frustum et chaque coordonnée comprise dans cette boîte sera affichée. Le processus qui convertit les coordonnées d’un intervalle spécifié en coordonnées normalisées pour être facilement transformées en coordonnées 2D de l’espace de vue est une projection.
L’opération finale appelée division de perspective, divise les composantes x, y et z des vecteurs position par la composante homogène w ; la division de perspective transforme l’espace de clipping 4D en coordonnées normalisées 3D. Cela se fait automatiquement à la fin de chaque passage dans le vertex shader.
Après cette étape, les coordonnées résultantes sont projetées en coordonnées écran et transformées en fragments.
La matrice de projection qui transforme les coordonnées de vue en coordonnées écran peut prendre deux formes différentes. On peut utiliser une projection orthogonale ou une projection en perspective.
10-5-1. Projection orthogonale▲
Une projection orthogonale définit un frustrum en forme de cube. Dans ce cas, on spécifie les dimensions du cube (largeur, hauteur, longueur). Les coordonnées qui sont à l’intérieur de ce cube ne seront pas clippées. Ce cube ressemble à un container :
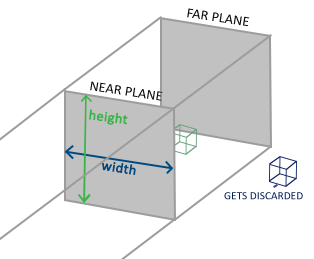
La composante w de chaque vecteur est inchangée. Si la composante w vaut 1.0, la division de perspective ne modifie pas les coordonnées.
Pour créer une matrice de projection orthogonale, on utilisera la fonction glm::ortho() :
glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);Les deux premiers paramètres spécifient les coordonnées gauche et droite du frustrum, ensuite on trouve les coordonnées bas et haut de ce frustrum. Les paramètres 5 et 6 donnent la position du plan avant et du plan arrière. Cette matrice de projection transforme toutes les coordonnées en coordonnées normalisées.
Cette projection directe produit des effets peu réalistes car il n’y a aucun effet de perspective. Pour cela on utilisera plutôt la projection en perspective.
10-5-2. Projection en perspective▲
Dans un dessin réaliste, les objets éloignés sont plus petits que les objets proches. C’est l’effet de perspective, que l’on voit bien sur l’image suivante :
On voit que les travées du rail se rapprochent lorsque la distance augmente. Cet effet est rendu par une matrice de projection en perspective. Cette matrice modifie la composante w de chaque sommet de telle façon que plus le sommet sera loin, plus w sera grand. Une fois les coordonnées transformées dans l’espace de clipping, elles sont dans l’intervalle [-w, +w]. OpenGL requiert que les coordonnées visibles soient entre -1 et +1. Lorsque les coordonnées sont dans l’espace de clipping, la division de perspective est appliquée à ces coordonnées en les divisant par w, résultant en valeurs d’autant plus faibles que les points sont éloignés du spectateur. Les coordonnées sont ensuite normalisées. Cela est détaillé dans cet excellent article de Songho.
Une matrice de projection en perspective peut être créée comme suit :
glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width/(float)height, 0.1f, 100.0f);Le rôle de glm::perspective() consiste à créer un frustrum qui définit l’espace visible, pouvant être vu comme une boîte de section variable :
Le premier paramètre définit le champ de vision (field of view (fov)) définissant l’angle d’ouverture de la boîte, souvent choisi à 45°, mais on peut changer cette valeur. Le second paramètre définit le rapport largeur/hauteur, les autres paramètres sont relatifs à la position des plans avant et arrière de la boîte.
Si la valeur near (plan avant de la boîte) est un peu trop grande (par exemple 10.0), les objets proches deviendront invisibles ce qui donne l’impression de voir au travers de ces objets si l’on s’en approche trop.
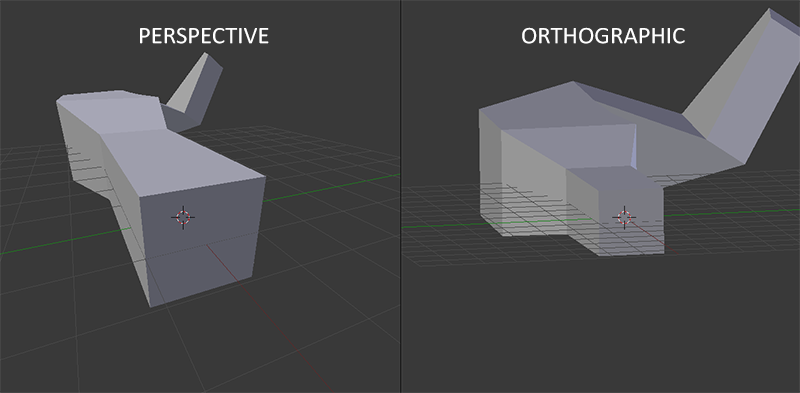
La projection orthogonale est souvent utilisée pour les rendus 2D et dans certaines applications d’ingénierie ou d’architecture quand on ne souhaite aucune distorsion due à la perspective. Des applications comme Blender utilisent ce type de projection pour la modélisation. On peut voir sur l’image suivante la différence entre les deux types de rendu :
10-6. Synthèse▲
Nous allons créer une matrice pour chaque étape mentionnée : modèle, vue et projection. Une coordonnée de sommet sera donc transformée comme suit :
kitxmlcodelatexdvpV_{clip} = M_{projection} \cdot M_{vue} \cdot M_{modele} \cdot V_{local}finkitxmlcodelatexdvpNoter que l’ordre de multiplication des matrices est inversé (on lit la multiplication des matrices de droite à gauche). Le sommet résultant sera ensuite affecté à la variable gl_Position dans le vertex shader et OpenGL réalisera ensuite automatiquement la division de perspective et le clipping.
Et ensuite ?
La sortie du vertex shader requiert que les coordonnées soient dans l’espace de clipping, ce que nous avons réalisé avec les matrices de transformation. OpenGL réalise la division de perspective et le clipping puis utilise les paramètres de glViewPort() pour obtenir les coordonnées écran à partir des NDC. Chaque coordonnée correspond donc à un point de l’écran. C’est la transformation de la zone de dessin.
Ce sujet peut vous paraître délicat, pas d’inquiétude, nous verrons comment utiliser ces concepts correctement, en particulier au travers des nombreux exemples.
10-7. Passons en 3D▲
Maintenant que nous savons comment transformer les coordonnées 3D en coordonnées 2D, nous allons commencer à montrer des objets plus réalistes que de simples plans 2D.
Commençons par créer une matrice de modèle, qui consistera ici en translations, homothéties et rotations permettant de placer nos sommets dans l’espace monde. Transformons notre plan en le faisant tourner selon l’axe X :
glm::mat4 model;
model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));En multipliant les coordonnées des sommets par cette matrice de modèle, nous transformons les coordonnées des sommets en coordonnées monde. Notre plan qui est un peu tourné vers le sol représente le plan dans l’espace monde.
Nous créons ensuite une matrice de vue. Nous voulons reculer un peu dans la scène de façon à ce que les objets deviennent visibles (dans l’espace monde, nous sommes situés à l’origine (0, 0, 0)). Se déplacer en arrière revient à faire avancer la scène, et donc déplacer les objets vers les z négatifs.
Système de coordonnées direct
La figure montre le repère utilisé par OpenGL, l’axe Z est dirigé vers nous :
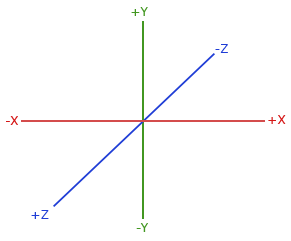
On peut se repérer de la façon suivante :
- placer le pouce de la main droite selon l'axe X ;
- placer l’index suivant l'axe Y ;
- le majeur vous indique alors le sens de l’axe Z.
Si vous utilisez la main gauche, ce sera le contraire…, le système inverse est utilisé dans DirectX. Notons que pour les coordonnées normalisées, OpenGL utilise le système inversé. (la matrice de projection inverse le système).
Nous verrons dans le prochain tutoriel comment déplacer le point de vue, mais pour l’instant notre matrice de vue sera la suivante :
glm::mat4 view;
view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));La dernière chose à faire est de définir la matrice de projection en perspective :
glm::mat4 projection;
projection = glm::perspective(glm::radians(45.0f), screenWidth / screenHeight, 0.1f, 100.0f);Nous devons ensuite passer ces matrices de transformation au shader. Déclarons ces matrices en variables uniformes, et modifions les sommets au moyen de ces matrices :
#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;
void main()
{
// notez que nous lisons la multiplication de droite à gauche
gl_Position = projection * view * model * vec4(aPos, 1.0);
...
}Nous devons aussi transmettre ces matrices au shader, cela à chaque rendu, car ainsi nous pourrons les modifier au cours du temps :
int modelLoc = glGetUniformLocation(ourShader.ID, "model"));
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // pareil pour View Matrix et Projection MatrixNos sommets sont ainsi modifiés par ces trois matrices, l’objet final devrait être :
- penché vers le sol ;
- un peu éloigné de nous ;
- affiché en perspective.
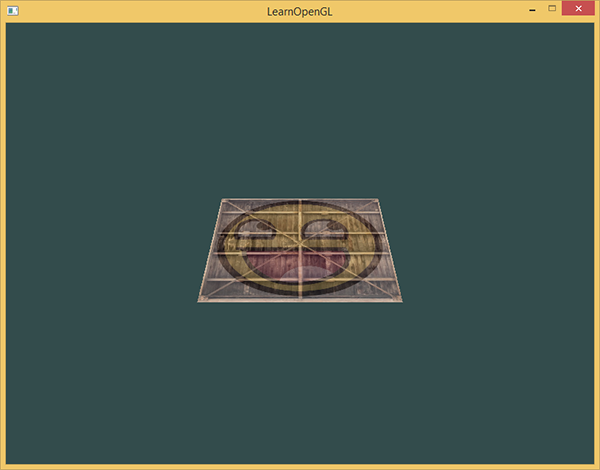
Voyons si le résultat correspond à cela :
Cela ressemble à un plan reposant sur un sol imaginaire. Vous pouvez vérifier votre code ici : source code.
10-8. Plus de 3D▲
Nous avons travaillé avec un plan 2D dans un espace 3D, passons maintenant à un cube en 3D. Pour cela nous utilisons 36 sommets (6 faces, 2 triangles par face, 3 sommets par triangle). Vous pouvez les retrouver ici. Pour le fun, faisons tourner ce cube :
model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f), glm::vec3(0.5f, 1.0f, 0.0f));Et ensuite, il faut afficher le cube avec ses 36 sommets :
glDrawArrays(GL_TRIANGLES, 0, 36);Vous devriez voir ceci :
Cela ressemble à un cube mais il reste un problème. Certaines faces du cube sont tracées par-dessus d’autres faces, cela parce qu’OpenGL trace le cube triangle par triangle, effaçant certains triangles en affichant par-dessus, alors qu’ils devraient être cachés.
Heureusement, OpenGL mémorise l’information de profondeur dans ce qu’on appelle un z-buffer, ce qui permet d’afficher ou non un pixel. On peut donc configurer OpenGL pour effectuer des tests de profondeur.
10-8-1. Z-buffer▲
OpenGL mémorise les informations de profondeur dans un z-buffer aussi appelé tampon de profondeur (depth-buffer). GLFW crée automatiquement ce tampon. La profondeur de chaque fragment est mémorisée, et à chaque affichage de fragment, la profondeur est comparée avec la valeur mémorisée dans le z-buffer ; si le fragment est derrière cette valeur, le fragment n’est pas affiché. Cette opération s’appelle le test de profondeur (depth testing).
Cependant, il faut activer ce test de profondeur, qui n’est pas activé par défaut. Cela se fait avec glEnable(). glEnable() et glDisable() permettent d’activer ou d’inhiber certaines fonctionnalités d’OpenGL. Voilà comment activer le test de profondeur :
glEnable(GL_DEPTH_TEST);Il faut aussi effacer le tampon de profondeur avant chaque rendu, de la même façon que l’on efface le tampon de couleurs :
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);Voyons ce que cela donne :
Ça fonctionne ! Voir le code ici.
10-8-2. Plus de cubes !▲
Supposons que nous voulions afficher 10 cubes sur l’écran. Chaque cube sera identique aux autres, mais placés différemment et tournant chacun selon un axe différent. Nous n’avons pas à modifier la définition du cube ni à modifier le tableau d’attributs pour dessiner plus d’objets. La seule chose à faire est de changer pour chaque objet la matrice de modèle pour chacun de ces cubes.
Définissons un vecteur de translation qui spécifie la position de chaque cube dans un tableau de glm::vec3 :
glm::vec3 cubePositions[] = {
glm::vec3( 0.0f, 0.0f, 0.0f),
glm::vec3( 2.0f, 5.0f, -15.0f),
glm::vec3(-1.5f, -2.2f, -2.5f),
glm::vec3(-3.8f, -2.0f, -12.3f),
glm::vec3( 2.4f, -0.4f, -3.5f),
glm::vec3(-1.7f, 3.0f, -7.5f),
glm::vec3( 1.3f, -2.0f, -2.5f),
glm::vec3( 1.5f, 2.0f, -2.5f),
glm::vec3( 1.5f, 0.2f, -1.5f),
glm::vec3(-1.3f, 1.0f, -1.5f)
};Utilisons une matrice de modèle différente pour chaque cube. Le cube défini sera ainsi rendu 10 fois avec une matrice de modèle différente (nous ajoutons aussi une petite rotation à chaque fois).
glBindVertexArray(VAO);
for(unsigned int i = 0; i < 10; i++)
{
glm::mat4 model;
model = glm::translate(model, cubePositions[i]);
float angle = 20.0f * i;
model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
ourShader.setMat4("model", model);
glDrawArrays(GL_TRIANGLES, 0, 36);
}En cas de souci, voir le code ici : source.
10-9. Exercices▲
- Expérimenter les paramètres FoV et aspect-ratio de la fonction projection de GLM. Voir comment cela affecte le frustrum de la perspective.
- Jouer avec la matrice de vue dans différentes directions pour voir le changement de la scène. Imaginez cette matrice comme une caméra.
- Essayer de faire tourner les trois premiers containers en laissant les autres fixes, cela en utilisant la matrice de modèle : solution.
10-10. Remerciements▲
Ce tutoriel est une traduction réalisée par Jean-Michel Fray dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.