Apprendre OpenGL moderne

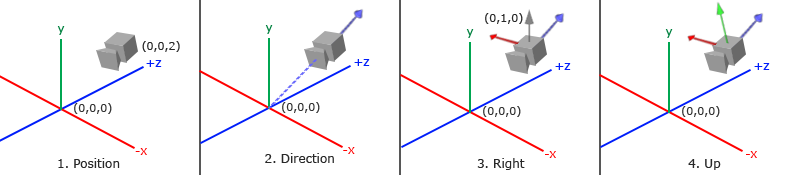
Lorsque nous parlons d’espace de vue, nous voyons toutes les coordonnées des sommets avec comme perspective celle de la caméra, prise comme origine. La matrice de vue transforme toutes les coordonnées en coordonnées de vue qui sont relatives à la position et à la direction de la caméra. Pour définir une caméra, nous devons connaître sa position, sa direction, un vecteur pointant vers la droite, un autre pointant vers le haut. Nous allons en fait créer un repère comprenant trois axes avec la caméra comme origine.

11-1-1. Position de la caméra▲

glm::vec3 cameraPos = glm::vec3(0.0f, 0.0f, 3.0f);

11-1-2. Direction de la caméra▲

glm::vec3 cameraTarget = glm::vec3(0.0f, 0.0f, 0.0f);
glm::vec3 cameraDirection = glm::normalize(cameraPos - cameraTarget);

11-1-3. Axe de droite▲

glm::vec3 up = glm::vec3(0.0f, 1.0f, 0.0f); 
glm::vec3 cameraRight = glm::normalize(glm::cross(up, cameraDirection));

11-1-4. Axe vers le haut▲

glm::vec3 cameraUp = glm::cross(cameraDirection, cameraRight);

Une propriété très intéressante des matrices est la suivante : si l’on définit trois axes perpendiculaires, on peut créer une matrice au moyen de ces trois axes, et en y ajoutant un vecteur de translation, on peut simplement changer de repère en multipliant les coordonnées d’un vecteur par cette matrice. C’est ce que fait la matrice LookAt pour obtenir les coordonnées dans l’espace de la caméra :

Où kitxmlcodeinlinelatexdvp\color{red}Rfinkitxmlcodeinlinelatexdvp est le vecteur pointant vers la droite, kitxmlcodeinlinelatexdvp\color{green}Ufinkitxmlcodeinlinelatexdvp le vecteur vers le haut, kitxmlcodeinlinelatexdvp\color{blue}Dfinkitxmlcodeinlinelatexdvp le vecteur dans la direction de visée et kitxmlcodeinlinelatexdvp\color{purple}Pfinkitxmlcodeinlinelatexdvp la position de la caméra. Notons que le vecteur est inversé puisque nous souhaitons déplacer l’espace dans la direction opposée au déplacement supposé du point de vue. En utilisant la matrice LookAt comme matrice de vue, nous transformerons toutes coordonnées de l’espace utilisé. Cette matrice crée ainsi une matrice de vue qui regarde dans la direction souhaitée.

En fait, GLM réalise déjà ce travail. Nous n’avons qu’à spécifier la position de la caméra ainsi qu’un point de visée et un vecteur qui pointe vers le haut et GLM fait le reste :

glm::mat4 view;
view = glm::lookAt(glm::vec3(0.0f, 0.0f, 3.0f), 
                   glm::vec3(0.0f, 0.0f, 0.0f), 
                   glm::vec3(0.0f, 1.0f, 0.0f));

La fonction glm::LookAt() requiert en paramètre la position, le point visé et le vecteur indiquant le haut. On crée ainsi une matrice de vue telle que définie dans le tutoriel précédent.

Avant de se plonger dans les entrées utilisateur, déplaçons notre caméra autour de la scène en gardant (0, 0, 0) comme point de visée.

Nous définissons comme position de la caméra un point situé sur un cercle, ce point étant modifié à chaque rendu, la caméra se déplace donc sur ce cercle de rayon radius. On recrée la matrice de vue à chaque fois, le rythme étant obtenu avec la fonction glfwGetTime() de GLFW :

float radius = 10.0f;
float camX = sin(glfwGetTime()) * radius;
float camZ = cos(glfwGetTime()) * radius;
glm::mat4 view;
view = glm::lookAt(glm::vec3(camX, 0.0, camZ), glm::vec3(0.0, 0.0, 0.0), glm::vec3(0.0, 1.0, 0.0));

Voilà le résultat :

Vous pouvez bien sûr essayer différentes valeurs de position et d’orientation pour mieux appréhender ces concepts. Le code se trouve ici.

Faire bouger la caméra autour de la scène est sympa, mais ce serait encore mieux si nous pouvions la déplacer nous-mêmes !

Créons d’abord une caméra en définissant les variables nécessaires au début du programme :

glm::vec3 cameraPos   = glm::vec3(0.0f, 0.0f,  3.0f);
glm::vec3 cameraFront = glm::vec3(0.0f, 0.0f, -1.0f);
glm::vec3 cameraUp    = glm::vec3(0.0f, 1.0f,  0.0f);

La fonction LookAt devient :

view = glm::lookAt(cameraPos, cameraPos - cameraFront, cameraUp);

Nous avons d’abord défini la caméra comme dans le paragraphe précédent. La direction est la position courante — le point de visée. Cela assure que la caméra visera toujours le point de visée. Modifions la position de la caméra en modifiant le vecteur cameraPos en utilisant le clavier. Nous avons déjà utilisé la fonction processInput() pour gérer les entrées clavier, ajoutons quelques nouvelles commandes :

void processInput(GLFWwindow *window)
{
    ...
    float cameraSpeed = 0.05f; // adjust accordingly
    if (glfwGetKey(window, GLFW_KEY_W) == GLFW_PRESS)
        cameraPos += cameraSpeed * cameraFront;
    if (glfwGetKey(window, GLFW_KEY_S) == GLFW_PRESS)
        cameraPos -= cameraSpeed * cameraFront;
    if (glfwGetKey(window, GLFW_KEY_A) == GLFW_PRESS)
        cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
    if (glfwGetKey(window, GLFW_KEY_D) == GLFW_PRESS)
        cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
}

En utilisant les touches WASD, la position de la caméra change : pour se déplacer en avant ou en arrière, on modifie le point de visée sur l’axe z, alors que les touches A et D permettent de se déplacer à droite ou à gauche de la position en cours.

On peut désormais faire bouger la caméra, à cela près que la vitesse est dépendante de votre système.

Nous avons choisi une valeur constante pour le mouvement, mais selon la rapidité de la machine on aura un résultat différent. Il faut pouvoir fixer la vitesse de déplacement de la caméra indépendamment de la rapidité de la machine.

Les applications graphiques et les jeux mémorisent en général le temps écoulé depuis le dernier rendu. On multiplie ensuite ce temps par les valeurs de vitesse. Si ce temps est grand (système lent), on augmente ainsi le déplacement à effectuer sur cette image et inversement, si le temps est petit (système rapide) on diminue le déplacement à effectuer pour cette image. Cela permet de s’affranchir de la vitesse de la machine.

Pour calculer ce temps, on utilisera deux variables globales :

float deltaTime = 0.0f; // Time between current frame and last frame
float lastFrame = 0.0f; // Time of last frame

On calcule ainsi pour chaque image le temps écoulé depuis le rendu précédent :

float currentFrame = glfwGetTime();
deltaTime = currentFrame - lastFrame;
lastFrame = currentFrame;

Et on tient compte de ce temps pour la vitesse de déplacement :

void processInput(GLFWwindow *window)
{
  float cameraSpeed = 2.5f * deltaTime;
  ...
}

On obtient ainsi une caméra plus douce et cohérente pour se déplacer :

Le code se trouve ici.

Utiliser les touches pour diriger son regard n’est pas très pratique. Mieux vaut utiliser la souris !

Nous allons modifier la direction visée en utilisant la souris. Cela est plus compliqué et requiert un peu de trigonométrie. Si vous n’êtes pas à l’aise avec ces notions, vous pouvez simplement recopier le code pour le moment.

11-5-1. Les angles d’Euler▲

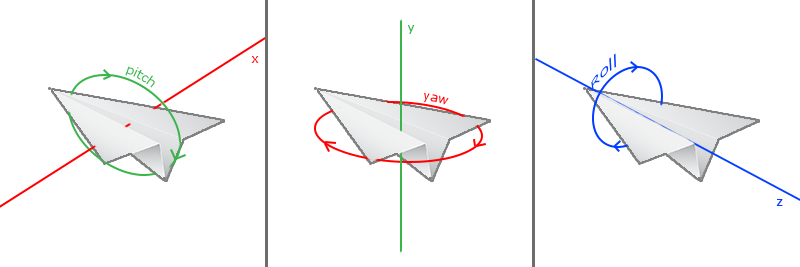
Les angles d’Euler sont trois valeurs qui permettent de représenter toute rotation en 3D. Pour mémoire, yaw = précession, pitch = nutation, roll = rotation propre.

Ces trois angles sont représentés sur la figure suivante :

Le pitch précise l’orientation vers le haut ou le bas, le yaw indique la rotation vers la droite ou la gauche. Le roll est par exemple utilisé dans les jeux de combat aérien, nous ne l’utiliserons pas ici. La combinaison de ces angles permet de calculer notre vecteur de rotation en 3D.

Pour notre système de caméra, nous n’avons besoin que du yaw et du pitch. Grâce à ces valeurs, nous pouvons obtenir un vecteur 3D représentant notre vecteur de direction. Le processus pour convertir le yaw et le pitch en un vecteur demande un peu de trigonométrie :

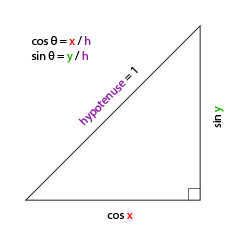
Si nous définissons l’hypoténuse à 1, nous savons grâce à la trigonométrie (cosinus, sinus, tangente) que la longueur du côté adjacent est kitxmlcodeinlinelatexdvp\cos \ \color{red}x/\color{purple}h = \cos \ \color{red}x/\color{purple}1 = \cos\ \color{red}xfinkitxmlcodeinlinelatexdvp et

kitxmlcodeinlinelatexdvp\sin \ \color{green}y/\color{purple}h = \sin \ \color{green}y/\color{purple}1 = \sin\ \color{green}yfinkitxmlcodeinlinelatexdvp pour le côté opposé. Cela nous donne des formules génériques pour obtenir la longueur de la direction sur l’axe des X et Y à partir d’un angle donné. Utilisons-les pour calculer les composantes du vecteur de direction :

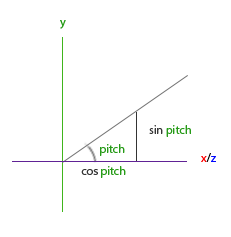
Le triangle ressemble au précédent. En le visualisant à partir du plan XZ et en regardant en direction de l’axe Y nous pouvons calculer la longueur de la direction Y (orientation verticale du regard). À partir de l’image, nous pouvons déduire que la valeur Y pour un pitch donné correspond à kitxmlcodeinlinelatexdvp\sin\ \thetafinkitxmlcodeinlinelatexdvp :

 

Sélectionnez

direction.y = sin(glm::radians(pitch)); // Notez que nous devons convertir les angles en radians

Ici, nous ne nous occupons que de la valeur Y, mais avec un peu plus de travail nous pouvons voir que les composantes X et Z sont aussi concernées. À partir du triangle, nous pouvons définir leurs valeurs comme suit :

 

Sélectionnez

direction.x = cos(glm::radians(pitch));
direction.z = cos(glm::radians(pitch));

Voyons si nous pouvons aussi trouver les composantes à partir du yaw :

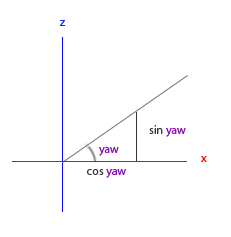
Tout comme avec le triangle pour le pitch, nous pouvons voir que la composante X dépend de kitxmlcodeinlinelatexdvpcos(yaw)finkitxmlcodeinlinelatexdvp et que la composante Z dépend de kitxmlcodeinlinelatexdvpsin(yaw)finkitxmlcodeinlinelatexdvp. En ajoutant ce constat au calcul précédent, nous pouvons obtenir le vecteur direction grâce aux valeurs du pitch et du yaw :

 

Sélectionnez

direction.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));
direction.y = sin(glm::radians(pitch));
direction.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));

Cela nous donne la formule pour convertir les valeurs de yaw et pitch en un vecteur direction que nous utiliserons pour inspecter la scène. Mais comment obtenir ces valeurs de pitch et yaw ?

Les valeurs yaw et pitch vont être obtenues en bougeant la souris (ou un joystick). Les mouvements horizontaux déterminent le yaw et les mouvements verticaux le pitch. Le principe consiste à mémoriser la position de la souris lors du dernier rendu et de calculer la différence de position de la souris lors du rendu en cours. La variation de position sera ensuite convertie en variation des angles yaw et pitch, ce qui se traduira par le mouvement correspondant de la caméra.

Tout d’abord, imposons à GLFW de cacher le curseur de la souris et de le capturer (une fois que l’application a le focus, le curseur restera dans la fenêtre jusqu’à ordre contraire ou fin de l’application). Cela se fait simplement :

glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_DISABLED);

Dès lors, la souris ne sera plus visible et ne quittera plus la fenêtre. C’est parfait pour une caméra à la première vue (comme dans les First Person Shooter (FPS)).

Nous devons imposer à GLFW d’enregistrer les événements correspondant aux mouvements de la souris, grâce à une fonction callback :

void mouse_callback(GLFWwindow* window, double xpos, double ypos);

Ici, xpos et ypos représentent la position de la souris. La fonction callback, une fois enregistrée, est appelée dès que la souris bouge. Pour l’enregistrer :

glfwSetCursorPosCallback(window, mouse_callback);

Pour gérer une caméra FPS au moyen de la souris, plusieurs étapes sont nécessaires avant de calculer la nouvelle direction de la caméra :

1. Calculer le déplacement de la souris depuis le dernier rendu ;
2. Ajouter ce déplacement aux angles yaw et pitch ;
3. Contraindre les angles à certaines valeurs limites ;
4. Calculer le nouveau vecteur direction.

Calculons le déplacement de la souris depuis le dernier rendu. On supposera au début que la souris est au milieu de la fenêtre (800 x 600) :

float lastX = 400, lastY = 300;

Puis nous calculons à chaque rendu le déplacement :

float xoffset = xpos - lastX;
float yoffset = lastY - ypos; // il faut inverser car ypos est donné de haut en bas
lastX = xpos;
lastY = ypos;

float sensitivity = 0.05f;
xoffset *= sensitivity;
yoffset *= sensitivity;

Nous utilisons une variable de sensibilité pour adapter la valeur du déplacement de la souris au déplacement de la caméra, cette sensibilité pouvant être réglée à votre convenance.

Nous mettons à jour les angles en fonction de ce déplacement :

yaw   += xoffset;
pitch += yoffset;

Il faut aussi contraindre les angles pour ne pas obtenir de mouvements bizarres de la caméra. Ainsi le pitch sera limité à [-89, +89] degrés, permettant de regarder le ciel ou le sol, mais pas de retourner la caméra.

if(pitch > 89.0f)
  pitch =  89.0f;
if(pitch < -89.0f)
  pitch = -89.0f;

Le yaw n’a pas besoin d’être limité, car on peut tourner horizontalement autant que l’on veut.

La dernière opération consiste à mettre à jour le vecteur direction avec ces nouveaux angles :

glm::vec3 front;
front.x = cos(glm::radians(pitch)) * cos(glm::radians(yaw));
front.y = sin(glm::radians(pitch));
front.z = cos(glm::radians(pitch)) * sin(glm::radians(yaw));
cameraFront = glm::normalize(front);

Le vecteur cameraFront est déjà inclus dans la matrice lookAt de GLM, pas besoin d’en faire plus.

Si vous exécutez le code, vous remarquerez que la caméra fait un grand bond dès que l’application est activée. Cela est dû à ce que la position initiale du curseur est fausse puisque définie au centre de la fenêtre, point assez éloigné du bord de la fenêtre où apparaît le curseur lorsque l’on donne le focus à l’application. Il faut, pour résoudre cela, initialiser correctement la position du curseur et ne pas effectuer de déplacement lors du premier rendu :

if(firstMouse) // variable initialisée à true, puis laissée à false
{
    lastX = xpos;
    lastY = ypos;
    firstMouse = false;
}

Le code final devient donc :

void mouse_callback(GLFWwindow* window, double xpos, double ypos)
{
    if(firstMouse)
    {
        lastX = xpos;
        lastY = ypos;
        firstMouse = false;
    }
  
    float xoffset = xpos - lastX;
    float yoffset = lastY - ypos; 
    lastX = xpos;
    lastY = ypos;

    float sensitivity = 0.05;
    xoffset *= sensitivity;
    yoffset *= sensitivity;

    yaw   += xoffset;
    pitch += yoffset;

    if(pitch > 89.0f)
        pitch = 89.0f;
    if(pitch < -89.0f)
        pitch = -89.0f;

    glm::vec3 front;
    front.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));
    front.y = sin(glm::radians(pitch));
    front.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));
    cameraFront = glm::normalize(front);
}

Voilà, on peut se déplacer librement dans la scène !

Pour compléter le système de caméra, nous allons ajouter un zoom. Dans le tutoriel précédent, nous avons vu que le champ de vision (fov) définit quelle proportion de la scène serait visible. Lorsque l’on diminue le fov, l’espace rendu devient aussi plus petit, donnant l’illusion d’un zoom. Nous utiliserons la roulette de la souris (scroll) pour régler ce zoom. On utilise à nouveau une fonction callback :

void scroll_callback(GLFWwindow* window, double xoffset, double yoffset)
{
  if(fov >= 1.0f && fov <= 45.0f)
        fov -= yoffset;
  if(fov <= 1.0f)
        fov = 1.0f;
  if(fov >= 45.0f)
        fov = 45.0f;
}

La valeur yoffset représente la variation de la roulette, et nous modifions le fov en conséquence. 45 degrés est la valeur par défaut pour le fov, nous allons donc le limiter entre 1.0 et 45.0.

Il faut ensuite modifier la matrice de projection en perspective avec cette nouvelle valeur du fov :

projection = glm::perspective(glm::radians(fov), 800.0f / 600.0f, 0.1f, 100.0f);

Et n’oublions pas d’enregistrer notre fonction callback :

glfwSetScrollCallback(window, scroll_callback);

Nous avons maintenant une caméra qui permet de se déplacer dans la scène à notre guise.

Essayez de coder ce système de caméra et de vous familiariser avec, en cas de souci le code est là : source code.

Une caméra nécessite pas mal de lignes de code, que nous réutiliserons dans la suite. Pour cette raison, nous allons concevoir une classe Camera qui fera le travail demandé, et nous allons même y ajouter quelques trucs. Nous allons juste vous donner le code de cette classe si vous souhaitez vous y plonger.

De la même façon que pour la classe Shader, nous créons cette classe dans un fichier d’en-tête. Vous le trouverez : ici. Vous pouvez comprendre le fonctionnement de cette classe, et on vous conseille de l’utiliser pour voir comment on peut créer un objet caméra de cette façon.

La version du code utilisant cette nouvelle caméra est ici.

• Voyez si vous pouvez transformer la classe Camera pour réaliser une vraie caméra FPS avec laquelle on ne peut pas voler, mais qui permet seulement de regarder la scène en restant dans le plan xz : solution.
• Essayez de créer votre propre fonction LookAt en créant manuellement une matrice de vue comme discuté au début de ce chapitre. Remplacer la fonction LookAt par la vôtre et voyez si cela fonctionne de la même façon : solution.

Ce tutoriel est une traduction réalisée par Jean-Michel Fray dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.