I. Test de profondeur (depth testing)▲
Dans le tutoriel sur les systèmes de coordonnées, nous avons affiché un conteneur 3D et nous avons utilisé le tampon de profondeur (depth buffer) pour éviter que les faces arrière ne s’affichent devant les autres. Dans ce tutoriel, nous allons approfondir cette notion de profondeur. Les valeurs de profondeur sont stockées dans un tampon spécifique, dit tampon de profondeur (ou z-buffer). Nous verrons aussi comment ce tampon est utilisé pour déterminer si un fragment est derrière les autres.
Le tampon de profondeur est un tampon qui, tout comme le tampon de couleurs (qui stocke les couleurs de tous les fragments : le résultat visuel), stocke une information par fragment et a (généralement) la même largeur et hauteur que le tampon de couleur. Le tampon de profondeur est automatiquement créé par le système de fenêtrage et stocke les valeurs de profondeur à l’aide de nombres à virgule flottante sur 16, 24 ou 32 bits. La plupart des systèmes l’utilisent avec une précision sur 24 bits.
Lorsque le test de profondeur est activé, OpenGL teste la valeur de la profondeur du fragment avec le contenu du tampon de profondeur. OpenGL effectue un test de profondeur et, si le test réussit, le tampon de profondeur est mis à jour avec la nouvelle valeur de profondeur. Si le test échoue, le fragment est abandonné.
Le test de profondeur est effectué dans l’espace écran après l’exécution du fragment shader (et après le test de pochoir (stencil) que nous allons voir dans le tutoriel suivant). Les coordonnées de l’espace écran correspondent directement à la zone de rendu définie avec la fonction glViewport() d’OpenGL et est accessible en GLSL dans le fragment shader avec la variable gl_FragCoord. Les composants x et y de gl_FragCoordreprésentent les coordonnées du fragment dans l’espace écran (avec (0, 0) en bas à gauche). La variable gl_FragCoord contient aussi un composant z qui détermine la valeur de profondeur du fragment. Ce z est la valeur utiliser dans la comparaison avec le contenu du tampon de profondeur.
Aujourd’hui, la plupart des GPU supportent une fonctionnalité appelée test de profondeur anticipé (early depth testing). Cette technique permet d’exécuter le test de profondeur avant l’exécution du fragment shader. Chaque fois qu’il est évident qu’un fragment ne sera pas visible (il est derrière d’autres objets), nous pouvons ignorer le fragment plus tôt.
Il est préférable de ne pas exécuter un fragment shader autant que faire se peut. L’optimisation n’est applicable que si vous ne définissez pas la valeur de la profondeur dans le fragment shader. Dans le cas contraire, il n’est pas possible de deviner la valeur pour effectuer le test de profondeur.
Le test de profondeur est désactivé par défaut et vous devez l’activer en utilisant l’option GL_DEPTH_TEST :
glEnable(GL_DEPTH_TEST);Une fois activé, OpenGL stocke automatiquement les valeurs de la composante z dans le tampon de profondeur suivant le résultat du test. Si le test échoue, le fragment est abandonné. Si vous avez activé le test de profondeur, vous devez nettoyer le tampon avant chaque rendu à l’aide de GL_DEPTH_BUFFER_BIT, sinon vous garderez les valeurs du rendu précédent :
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);Il existe certains scénarios où vous souhaitez effectuer le test de profondeur sur tous les fragments, mais sans mettre à jour le tampon de profondeur. En soi, vous avez un tampon de profondeur en lecture seule. OpenGL nous permet d’activer ou non l’écriture dans le tampon de profondeur en définissons le masque à GL_FALSE :
glDepthMask(GL_FALSE);Évidemment, cela n’a d’effet que si le test de profondeur est actif.
I-A. Fonction de test▲
OpenGL permet de modifier l’opérateur de comparaison utilisé dans le test de profondeur. Cela permet de contrôler dans quel cas le test de profondeur réussit et dans quel cas les fragments sont abandonnés et quand mettre à jour le tampon. Nous pouvons définir l’opérateur de comparaison (ou fonction de profondeur) en appelant glDepthFunc() :
glDepthFunc(GL_LESS);Voici la liste des opérateurs de comparaison possibles :
|
Fonction |
Description |
|
GL_ALWAYS |
Le test de profondeur réussit toujours |
|
GL_NEVER |
Le test de profondeur ne réussit jamais |
|
GL_LESS |
Le test réussit si la valeur du fragment est inférieure à la valeur dans le tampon |
|
GL_EQUAL |
Le test réussit si la valeur du fragment est égale à la valeur dans le tampon |
|
GL_LEQUAL |
Le test réussit si la valeur du fragment est inférieure ou égale à la valeur dans le tampon |
|
GL_GREATER |
Le test réussit si la valeur du fragment est supérieure à la valeur dans le tampon |
|
GL_NOTEQUAL |
Le test réussit si la valeur du fragment est différente de la valeur dans le tampon |
|
GL_GEQUAL |
Le test réussit si la valeur du fragment est supérieure ou égale à la valeur dans le tampon |
La fonction par défaut est GL_LESS. Cela signifie que tous les fragments dont la valeur de profondeur est supérieure ou égale à la valeur dans le tampon sont abandonnés.
Voyons l’impact de la fonction de profondeur. Nous allons utiliser une nouvelle configuration qui affiche une scène simple avec deux cubes texturés posés sur un sol texturé sans éclairage. Vous pouvez trouver le code source ici.
Dans le code, nous changeons la fonction de profondeur à GL_ALWAYS :
glEnable(GL_DEPTH_TEST);
glDepthFunc(GL_ALWAYS);Cela revient à ne pas avoir activé le test de profondeur. Le test réussit toujours, donc les fragments qui sont affichés en dernier seront devant les fragments affichés avant, même s’ils auraient dû être derrière. Comme nous avons dessiné le sol à la fin, ses fragments recouvrent ceux des cubes :
En remettant GL_LESS, cela donne le type de scène auquel nous étions habitués :
I-B. Précision du test de profondeur▲
Le tampon de profondeur contient des valeurs entre 0.0 et 1.0. Ces valeurs sont comparées avec la composante z des objets de la scène comme vu par le spectateur. Ces valeurs z dans l’espace vue peuvent prendre n’importe quelle valeur entre le plan proche (near) et le plan lointain (far) déterminé par la projection. Nous devons donc trouver une méthode pour transformer ces valeurs provenant de l’espace vue vers l’échelle [0, 1]. Une méthode est de les transformer linéairement. L’équation (linéaire) suivante transforme la valeur z pour obtenir une valeur entre 0.0et 1.0 :
kitxmlcodelatexdvpF_{depth} = \frac{z - near}{far - near}finkitxmlcodelatexdvpIci, near et far sont les valeurs que nous avons utilisées pour créer la matrice de projection (voir le chapitre sur les systèmes de coordonnées). L’équation prend une valeur z présente dans le champ de vision et la transpose dans l’échelle [0, 1]. La relation entre la valeur z et la profondeur correspondante est présentée sur ce graphique suivant :
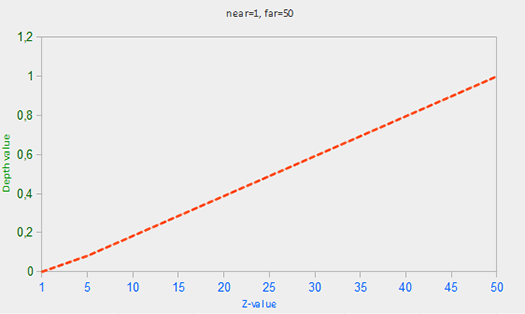
Toutes les équations donnent une valeur proche de 0.0 lorsque l’objet est proche et une valeur de profondeur proche de 1.0 lorsque l’objet s’approche du plan lointain.
Toutefois, un tampon de profondeur linéaire n’est pratiquement jamais utilisé. Pour obtenir des propriétés de projection correctes, une équation non linéaire proportionnelle à kitxmlcodeinlinelatexdvp\frac{1}{z}finkitxmlcodeinlinelatexdvp est utilisée . Cela permet d’obtenir une très grande précision lorsque le z est petit et une plus faible précision lorsque l’objet est loin. Pensez-y une seconde : avons-nous vraiment besoin de la même précision pour un objet éloigné de 1000 unités et un objet proche ? L’équation linéaire ne fait pas ce genre de considérations.
Comme la fonction non linéaire est proportionnelle à kitxmlcodeinlinelatexdvp\frac{1}{z}finkitxmlcodeinlinelatexdvp, les valeurs entre 1.0 et 2.0 donneront des valeurs entre 1,0 et 0,5, soit la moitié de la précision disponible. De même, des valeurs de z entre 50,0 et 100,0 ne prendront que 2 % de la précision disponible. Voici l’équation permettant de prendre en compte les distances near et far :
kitxmlcodelatexdvpF_{depth} = \frac{\frac{1}{z} - \frac{1}{near}}{\frac{1}{far} - \frac{1}{near}}finkitxmlcodelatexdvpNe vous inquiétez pas si vous ne comprenez pas ce que fait l’équation. La chose à retenir est que les valeurs dans le tampon de profondeur ne sont pas linéaires dans l’espace écran (elles sont linéaires dans l’espace vue, avant que la matrice de projection ne soit appliquée). Une valeur de 0,5 dans le tampon de profondeur ne veut pas dire que la valeur z de l’objet est à la moitié du champ de vision. La valeur z du sommet est en réalité assez proche du spectateur ! Vous pouvez voir la relation entre les valeurs z et leur correspondance dans le graphique suivant :
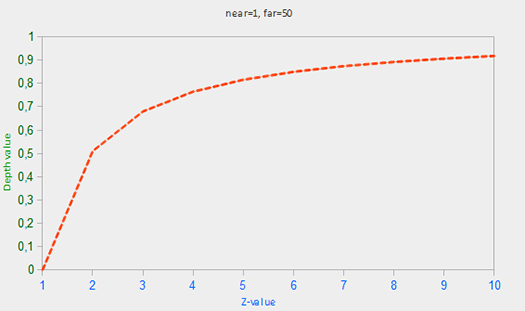
Comme vous pouvez le voir, les valeurs de profondeur sont principalement déterminées par les petites valeurs de z, donnant ainsi une grande précision pour les objets proches. L’équation pour transformer les valeurs z (du point de vue du joueur) est embarquée dans la matrice de projection. Par conséquent, lors de la transformation des coordonnées de sommets de l’espace vue à l’espace de découpage, puis à l’espace écran, l’équation non linéaire est appliquée. Si vous êtes curieux de comprendre ce que fait réellement la matrice de projection, je vous suggère de lire l’article de .
L’effet de l’équation non linéaire devient très visible lorsque nous essayons d’afficher le tampon de profondeur.
I-C. Visualisation du tampon de profondeur▲
Nous savons que la valeur z de la variable du fragment shader gl_FragCoord contient la valeur de profondeur pour un fragment en particulier. Si nous utilisons la valeur de profondeur du fragment comme une couleur, nous pouvons afficher les valeurs du tampon de profondeur de l’intégralité de la scène. Nous pouvons le faire en retournant une nuance de gris basée sur la valeur de profondeur :
void main()
{
FragColor = vec4(vec3(gl_FragCoord.z), 1.0);
}Si vous exécutez le même programme, vous allez sûrement voir que tout est blanc, comme si toutes les valeurs de profondeur sont à 1.0, soit la valeur de profondeur maximale. Pourquoi ?
Vous devez garder en tête ce que nous avons vu dans la précédente section : les valeurs de profondeur en espace écran ne sont pas linéaire, c’est-à-dire, que la précision est plus importante pour les petites valeurs de z. La valeur de profondeur augmente rapidement suivant la distance, tous les sommets sont donc proches d’une profondeur de 1,0. Si nous nous approchions des objets, nous pourrions éventuellement obtenir des couleurs plus sombres et donc des valeurs de z plus faibles :
Cela met en évidence la non-linéarité des valeurs de profondeur. Les objets proches ont un impact plus important sur les valeurs que les objets au loin. En se déplaçant seulement de quelques millimètres, les couleurs passent du noir au blanc.
Toutefois, nous pouvons transformer les valeurs non linéaires en leur correspondance linéaire. Pour ce faire, nous devons refaire à l’envers le procédé de la projection uniquement pour les valeurs de profondeur. Cela signifie que nous devons repasser les valeurs allant de 0 à 1 en des valeurs allant de -1 à 1 (espace de découpage). Ensuite, nous devons enlever l’aspect non linéaire (deuxième équation) provenant de la matrice de projection et appliquer l’inverse de l’équation à la valeur de profondeur finale. Ainsi, nous obtenons des valeurs de profondeur linéaire. Cela semble-t-il faisable ?
Premièrement, nous transformons les valeurs de profondeur en coordonnées normalisées :
float z = depth * 2.0 - 1.0;Ensuite, nous prenons le résultat z et appliquons la transformation inverse pour obtenir une valeur de profondeur linéaire :
float linearDepth = (2.0 * near * far) / (far + near - z * (far - near));Cette équation est déduite à partir de la matrice de projection qui utilise l’équation non linéaire permettant d’obtenir les valeurs de profondeur entre near et far. Cet article mathématiquement imposant explique en détails la matrice de projection. Il explique aussi d’où vient l’équation.
Le fragment shader complet qui transforme la profondeur non linéaire de l’espace écran en profondeur linéaire correspond à :
#version 330 core
out vec4 FragColor;
float near = 0.1;
float far = 100.0;
float LinearizeDepth(float depth)
{
float z = depth * 2.0 - 1.0; // back to NDC
return (2.0 * near * far) / (far + near - z * (far - near));
}
void main()
{
float depth = LinearizeDepth(gl_FragCoord.z) / far; // division par far pour la démonstration
FragColor = vec4(vec3(depth), 1.0);
}Comme les valeurs entre near et far sont principalement supérieures à 1,0, elles sont affichées complètement en blanc. En divisant la profondeur linéaire par far dans la fonction main(), nous convertissons la profondeur pour obtenir des valeurs entre 0 et 1. Ainsi, nous pouvons voir les objets proches devenir progressivement plus clairs que les fragments proches du plan lointain.
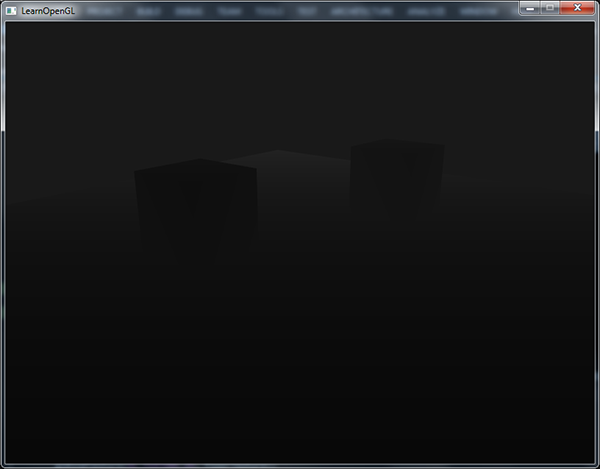
Si nous exécutons l’application, nous obtenons des valeurs de profondeur linéaire sur la distance. Essayez d’explorer la scène pour voir les valeurs changer.
La scène est principalement noire, car le plan proche est à 0,1 et le plan lointain à 100, ce qui est très éloigné. Le résultat est que les objets sont plutôt proches du plan proche et donc les valeurs de profondeur sont faibles (plus sombres).
I-D. Conflit de profondeur▲
Un problème visuel classique peut arriver lorsque deux plans ou triangles sont superposés et que le tampon de profondeur n’a pas assez de précision pour déterminer quel est celui devant l’autre. Les deux formes vont continuellement alterner et donner des artefacts visuels. Cela s’appelle un conflit de profondeur (z-fighting), car les formes semblent se battre pour être par-dessus l’autre.
Dans la scène de ce tutoriel, il y a quelques endroits où le conflit de profondeur peut arriver. Les conteneurs sont exactement placés à la même hauteur que le sol et donc leur face du dessous est coplanaire avec le plan du sol. Les valeurs de profondeur des deux plans sont les mêmes, ce qui fait que le test de profondeur n’a pas de méthode pour déterminer lequel est le bon.
Si vous déplacez la caméra dans l’un des conteneurs, vous allez vous vite en rendre compte : la face du dessous alterne constamment entre la face du conteneur et le sol :
Le conflit de profondeur est un problème courant avec les tampons de profondeur et il est généralement plus fort lorsque les objets sont lointains (car le tampon de profondeur a moins de précision pour ceux-ci). Le conflit de profondeur ne peut pas être complètement supprimé, mais il y a quelques astuces pour l’éviter.
I-D-1. Éviter le conflit de profondeur▲
La première et la plus importante astuce est de ne jamais placer des objets trop proches des autres pour éviter le recouvrement des triangles. En ajoutant un petit décalage entre deux objets, difficilement visible pour l’utilisateur, vous allez éviter complètement un conflit entre les deux objets. Dans le cas de cette scène, nous pouvions placer les conteneurs légèrement un peu plus haut. La différence est tellement faible qu’elle est difficilement constatable, mais elle évite les conflits de profondeur. Toutefois, cela nécessite une intervention manuelle sur chaque objet et des tests pour s’assurer que tous les cas sont évités.
Une deuxième astuce consiste à définir le plan proche aussi loin que possible. Dans l’une des précédentes sections, nous avons discuté de la précision qui est extrêmement grande pour les objets à proximité du plan proche. Si nous déplaçons ce plan un peu plus loin du joueur, nous allons grandement augmenter la précision sur l’intégralité du tronc (frustum). Toutefois, en définissant le plan proche trop loin, vous allez provoquer des coupures de vos objets proches. C’est donc un ajustement à faire avec précaution et justesse pour trouver la bonne distance pour le plan proche.
Une autre astuce coûteuse en termes de performance est d’utiliser un tampon de profondeur plus précis. La plupart des tampons de profondeur ont une précision de 24 bits, mais la plupart des cartes graphiques actuelles gèrent les tampons de profondeur sur 32 bits, ce qui augmente grandement la précision. En échange de performance, vous allez avoir une meilleure précision pour vos tests de profondeur et donc réduire les conflits.
Les trois techniques que nous avons vues sont les plus courantes et faciles à mettre en place pour éviter les conflits. Il en existe d’autres, nécessitant plus de travail et ne supprimant pas pour autant l’intégralité des cas de conflits. Les conflits de profondeur sont courants, mais si vous utilisez la bonne combinaison des techniques listées, vous allez probablement ne jamais vraiment avoir de vrais problèmes.
I-E. Remerciements▲
Ce tutoriel est une traduction réalisée par Alexandre Laurent dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.