Apprendre OpenGL moderne

Le plus souvent, la lumière ne provient pas d’une seule source mais de plusieurs, réparties autour de nous, même si elles ne sont pas immédiatement perceptibles. Une des propriétés de la lumière est de se refléter et de se diffuser dans toutes les directions, et pas seulement dans le voisinage direct de la source. La lumière se réfléchit sur les surfaces des objets et a un impact sur l’éclairage des autres objets. Les algorithmes qui traitent cet effet sont appelés algorithmes d’illumination globale, mais ils se révèlent complexes et gourmands.

Puisque nous ne sommes pas très enclins à ces algorithmes complexes, nous utiliserons un modèle simple d’illumination globale : l’éclairage ambiant. Comme nous l’avons vu dans le chapitre précédent, on utilisera une petite source lumineuse de couleur constante que nous ajouterons à la couleur finale des fragments de l’objet, donnant ainsi l’impression qu’il y a toujours un peu de lumière, même en l’absence de source directe de lumière.

Ajouter un éclairage ambiant à la scène est assez facile. Nous multiplions la couleur de la lumière par un petit facteur constant, et multiplions ensuite le résultat par la couleur des objets pour obtenir la couleur du fragment :

void main()
{
    float ambientStrength = 0.1;
    vec3 ambient = ambientStrength * lightColor;
    vec3 result = ambient * objectColor;
    FragColor = vec4(result, 1.0);
}

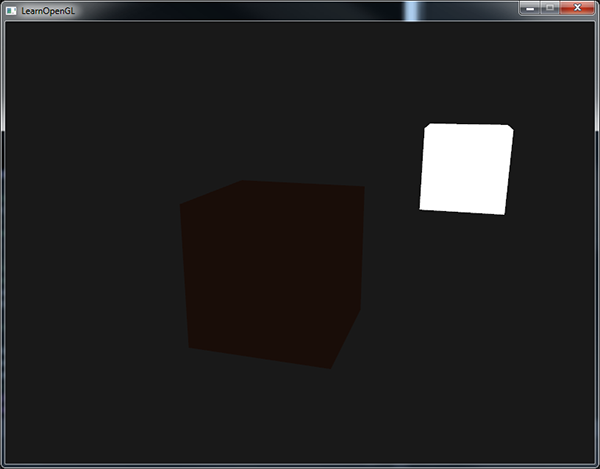
Si vous exécutez votre programme, vous noterez que la première étape de l’éclairage est appliquée à votre objet. L’objet est assez sombre, mais pas complètement grâce à cet éclairage ambiant (le cube lampe n’est pas affecté car il utilise un autre shader). Cela donne quelque chose comme ceci :

L’éclairage ambiant ne produit pas des effets passionnants ; par contre, l’éclairage diffus va commencer à produire des effets visuels significatifs. Cet éclairage diffus rendra l’objet d’autant plus lumineux que ses fragments seront alignés avec les rayons lumineux de la source. Pour mieux comprendre cet effet, regardons l’image suivante :

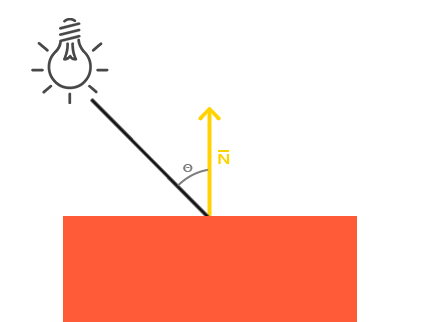
On voit sur la gauche une source de lumière qui émet un rayon en direction d’un fragment de notre objet. Nous mesurons l’angle avec lequel ce rayon arrive sur l’objet. Si le rayon lumineux arrive perpendiculairement à la surface de l’objet, il aura l’effet maximum. Pour mesurer cet angle d’incidence, nous utilisons un vecteur appelé vecteur normal (ou normale), qui est un vecteur perpendiculaire à la surface (figuré ici par une flèche jaune) ; nous reverrons cela plus tard. L’angle d’incidence peut alors facilement être calculé au moyen du produit scalaire.

Vous vous rappelez du chapitre sur les transformations où nous avions vu que plus l’angle entre deux vecteurs unitaires est faible, plus le produit scalaire s’approche de la valeur 1. Si les deux vecteurs sont perpendiculaires, ce produit vaut 0. Ici, plus l’angle θ sera grand, moins la lumière aura d’effet sur la couleur de l’objet.

Le produit scalaire retourne donc une valeur que nous utiliserons pour calculer l’effet de la lumière sur la couleur du fragment, résultant en des fragments éclairés différemment selon leur orientation par rapport aux rayons lumineux.

Pour calculer un éclairage diffus, il nous faudra :

• un vecteur normal : un vecteur perpendiculaire à la surface du fragment ;
• la direction de la lumière incidente, calculée comme la différence entre la position de la source et celle du fragment considéré.

II-B-1. Vecteur normal (ou normale)▲

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec3 aNormal;
...

glVertexAttribPointer(0, 3, GL_FLOAT, GL_FALSE, 6 * sizeof(float), (void*)0);
glEnableVertexAttribArray(0);

out vec3 Normal;
void main()
{
 gl_Position = projection * view * model * vec4(aPos, 1.0);
 Normal = aNormal;
}

in vec3 Normal;

II-B-2. Calcul de la composante diffuse▲

Nous disposons d’une normale pour chaque sommet, mais nous devons encore calculer la position de la source et celle des fragments. Puisque la source ne change pas de position, on utilisera une variable uniforme dans le fragment shader :

 

Sélectionnez

uniform vec3 lightPos;

Ensuite, initialisons cette variable dans la boucle d’affichage (ou ailleurs). On utilise le vecteur lightPos déclaré dans le chapitre précédent comme position de la source :

 

Sélectionnez

lightingShader.setVec3("lightPos", lightPos);

Enfin, nous devons connaître la position du fragment considéré. Nous ferons tous les calculs d’éclairage dans l’espace monde, nous souhaitons donc connaître la position des sommets dans cet espace. En multipliant les attributs de position des sommets uniquement par la matrice de modèle (et pas les matrices de vue ni de projection), on obtiendra les coordonnées dans l’espace monde. Cela peut être réalisé dans le vertex shader, déclarons donc une variable de sortie et calculons ces coordonnées dans l’espace monde :

 

Sélectionnez

out vec3 FragPos;
out vec3 Normal;
void main()
{
    gl_Position = projection * view * model * vec4(aPos, 1.0);
    FragPos = vec3(model * vec4(aPos, 1.0));
    Normal = aNormal;
}

Et ajoutons une variable d’entrée dans le fragment shader :

 

Sélectionnez

in vec3 FragPos;

Nous avons maintenant toutes les variables nécessaires pour les calculs d’éclairage dans le fragment shader.

Calculons d’abord le vecteur représentant la direction de la lumière entre la source et la position du fragment. Nous avons montré que ce vecteur peut être calculé par la différence entre la position de la source et celle du fragment. Comme nous l’avons vu dans le chapitre sur les transformations, il suffit d’effectuer la différence entre ces deux vecteurs. Nous voulons également utiliser des vecteurs unitaires, par conséquent nous normalisons le vecteur de direction et la normale :

 

Sélectionnez

vec3 norm = normalize(Normal);
vec3 lightDir = normalize(lightPos - FragPos);

Pour calculer l’éclairage, on n’a pas besoin de la longueur ni de la position des vecteurs, mais seulement de leur direction. On peut donc utiliser des vecteurs unitaires pour simplifier les calculs. Assurez-vous de normaliser les vecteurs pour effectuer ces calculs. Oublier cette opération est une erreur assez fréquente.

La composante diffuse de la lumière sur un fragment passe par le calcul du produit scalaire entre le vecteur norm et le vecteur lightDir. Le résultat est ensuite multiplié par la couleur de la lumière pour obtenir la composante diffuse, résultant en une lumière d’autant plus sombre que l’angle entre ces deux vecteurs est grand :

 

Sélectionnez

float diff = max(dot(norm, lightDir), 0.0);
vec3 diffuse = diff * lightColor;

Si l’angle entre les deux vecteurs est supérieur à 90°, le produit scalaire est négatif, ce qui donnerait une composante diffuse négative. Pour éviter cela, nous limitons le résultat aux valeurs positives en utilisant la fonction max. Les couleurs ne seront donc jamais négatives. Les couleurs négatives ne sont pas définies, mieux vaut s’en passer.

Nous disposons de la composante ambiante et de la composante diffuse de la lumière, nous ajoutons ces deux composantes et multiplions le résultat par la couleur de l’objet pour obtenir la couleur finale du fragment :

 

Sélectionnez

vec3 result = (ambient + diffuse) * objectColor;
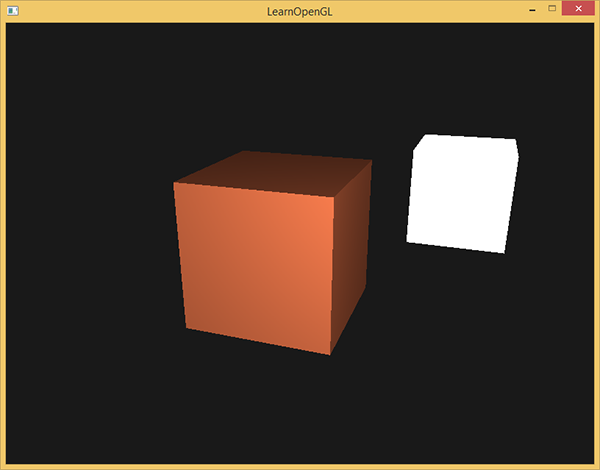
FragColor = vec4(result, 1.0);

Si votre application et vos shaders sont corrects, vous devriez obtenir cette image :

On voit qu’avec la lumière diffuse, le cube commence à devenir plus réaliste. Essayez de visualiser les normales mentalement et tournez autour du cube pour voir que plus l’angle d’incidence est grand, plus la surface est sombre.

En cas de besoin, vous pourrez trouver le code complet de cette partie ici.

II-B-3. Une dernière chose▲

Jusqu’ici, nous avons passé les normales directement du vertex shader au fragment shader. Cependant, les calculs que nous avons faits dans le fragment shader l’ont été avec les coordonnées de l’espace monde, ne devons-nous pas exprimer ces normales dans l’espace monde aussi ? Oui, mais ce n’est pas aussi simple qu’une multiplication par la matrice de modèle.

Tout d’abord, les normales ne représentent que des directions, sans position particulière dans l’espace. Ainsi, les normales n’ont pas de coordonnée homogène (la composante w de la position d’un sommet). Cela implique que les translations n’ont pas d’effet sur ces normales. Si nous souhaitons multiplier ces vecteurs par la matrice de modèle, il nous faut supprimer la partie translation de cette matrice en ne conservant que les trois premières lignes et les trois premières colonnes (on pourrait aussi donner la valeur 0 à la composante w de la normale et conserver une matrice 4x4). Les seules transformations que nous voulons effectuer sur les normales sont les homothéties et les rotations.

Ensuite, si la matrice de modèle effectuait une mise à l’échelle non uniforme, les normales ne seraient plus perpendiculaires aux surfaces, on ne pourrait donc pas utiliser une telle matrice de modèle pour transformer les normales. L’image suivante montre l’effet d’une telle matrice sur une normale :

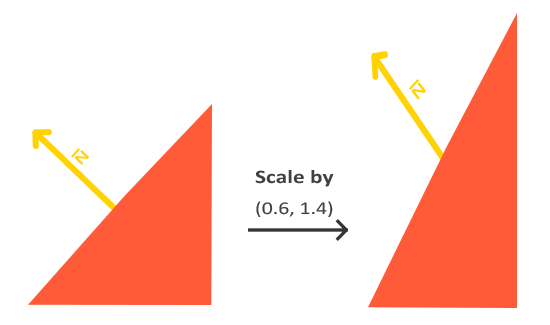
En appliquant une mise à l’échelle non uniforme, les normales ne sont plus perpendiculaires aux surfaces, ce qui fausse le calcul de la lumière (une mise à l’échelle uniforme ne modifie pas la direction des normales — ni celle des surfaces — mais juste leur longueur, ce qui n’est pas gênant puisque l’on normalise ces vecteurs).

L’astuce consiste à utiliser une matrice de modèle différente, spécifiquement conçue pour les normales. Cette matrice est appelée matrice de normale et utilise quelques opérations de l’algèbre linéaire pour éviter cet effet indésirable. Si vous souhaitez savoir comment est calculée cette matrice, je vous suggère de consulter cet article.

La matrice de normale est définie comme « la transposée de l’inverse du coin en haut à gauche de la matrice de modèle ». Pas simple, et si vous ne comprenez pas ce que cela veut dire, pas de souci : nous n’avons pas parlé de l’inversion ni de la transposition des matrices. Notez que la plupart des ressources sur le sujet définissent la matrice de normale en appliquant ces opérations sur la matrice modèle-vue, mais puisque nous travaillons dans l’espace monde (et non pas dans l’espace de vue), nous n’utiliserons que la matrice de modèle.

Dans le vertex shader, on peut générer cette matrice de normale nous-mêmes en utilisant les fonctions inverse et transpose. Notons que l’on projette notre matrice sur une matrice 3x3 pour écarter la translation et pouvoir la multiplier par un vecteur de normale vec3 :

 

Sélectionnez

Normal = mat3(transpose(inverse(model))) * aNormal;

Dans le paragraphe consacré à la lumière diffuse, l’éclairage était correct, mais nous n’avions réalisé aucune opération de mise à l’échelle sur l’objet et nous n’avions donc pas besoin d’une matrice de normale, la matrice de modèle était suffisante. Si par contre vous utilisez une mise à l’échelle non uniforme, il est essentiel de multiplier les normales par la matrice de normale.

L’inversion de matrices est une opération coûteuse, même pour les shaders, essayez d’éviter autant que possible ces opérations dans les shaders, car elles seront effectuées sur chaque sommet de la scène. Cela est intéressant pour apprendre, mais pour une application efficace, on effectuera ces calculs sur le CPU et on transmettra le résultat par une variable uniforme avant l’affichage (comme pour la matrice de modèle).

Si vous n’êtes pas trop fatigué avec ces calculs d’éclairage, nous pouvons aborder l’éclairage spéculaire pour compléter le modèle de Phong.

De même que l’éclairage diffus, l’éclairage spéculaire est basé sur la direction des rayons lumineux et les normales, mais cette fois il faut aussi tenir compte de l’angle avec lequel la surface du fragment est perçue, c’est-à-dire du point de vue du spectateur. L’éclairage spéculaire utilise les propriétés de réflexion de la lumière. Si nous considérons la surface d’un objet comme un miroir, l’éclairage spéculaire sera le plus fort dans la direction de réflexion. On peut voir cela sur la figure suivante :

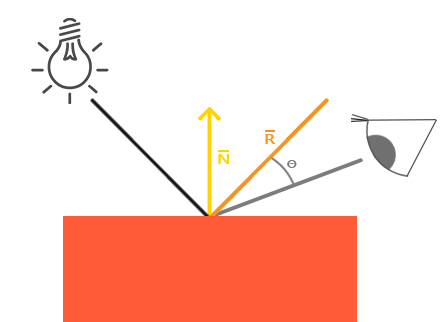
On calcule le vecteur de réflexion en symétrisant la direction de la lumière incidente par rapport à la normale. On calcule ensuite la distance angulaire entre cette direction de réflexion et la direction de vue. Plus ces deux directions seront proches, plus la composante spéculaire sera grande. L’effet résultant sera de voir une tache de lumière dans la direction de réflexion de la lumière incidente.

Le vecteur de vue est une variable de plus, nécessaire pour l’éclairage spéculaire, que nous pouvons calculer en utilisant l’espace monde du spectateur et la position des fragments. Ensuite, nous calculerons l’intensité spéculaire, nous multiplierons cela par la couleur de la lumière et on ajoutera le résultat à la lumière ambiante et à la lumière diffuse.

Pour obtenir les coordonnées du spectateur dans l’espace monde, il suffit d’utiliser le vecteur position de la caméra. Ajoutons donc une nouvelle variable uniforme au fragment shader et passons-lui la position de la caméra :

uniform vec3 viewPos;

lightingShader.setVec3("viewPos", camera.Position);

Nous disposons maintenant des variables nécessaires pour calculer l’intensité spéculaire. Premièrement, nous définissons une valeur d’intensité spéculaire pour donner à l’éclairage spéculaire une couleur moyennement brillante pour obtenir un effet modéré :

float specularStrength = 0.5;

Si nous donnions la valeur 1.0 à ce paramètre, nous aurions une composante très brillante, ce qui est un peu trop pour notre cube corail. Dans le prochain chapitre, nous verrons comment définir correctement ces propriétés et comment cela affecte les objets. Ensuite, nous calculons le vecteur de direction de la vue et le vecteur réflexion :

vec3 viewDir = normalize(viewPos – FragPos);
vec3 reflectDir = reflect(-lightDir, norm);

Notez que nous inversons le vecteur lightDir. La fonction reflect() demande à ce que le premier vecteur pointe de la source de lumière vers le fragment, alors que le vecteur lightDir pointe dans le sens inverse. Le second vecteur est le vecteur normal au fragment.

Il reste à calculer l’intensité de la composante spéculaire. On le réalise avec la formule suivante :

float spec = pow(max(dot(viewDir, reflectDir), 0.0), 32);
vec3 specular = specularStrength * spec * lightColor;

On calcule d’abord le produit scalaire entre la direction de vue et la direction de réflexion (en s’assurant que ce produit n’est pas négatif), et on élève le résultat à la puissance 32. Cette valeur 32 est la valeur de la brillance. Plus grande est cette valeur pour un objet, plus la lumière sera reflétée dans une direction précise et non diffusée dans toutes les directions. On peut voir dans l’image suivante l’influence de ce paramètre :

On ne souhaite pas que la composante spéculaire soit trop dominante, on choisit donc une valeur intermédiaire : 32. Il faut enfin ajouter cette composante spéculaire aux deux autres et multiplier le résultat par la couleur de l’objet :

vec3 result = (ambient + diffuse + specular) * objectColor;
FragColor = vec4(result, 1.0);

Nous avons donc calculé toutes les composantes du modèle de Phong. Voilà le résultat de ces calculs avec un certain point de vue :

Le code complet de l’application se trouve ici.

Vous commencez à voir la puissance des shaders. Avec peu d’information, les shaders sont en mesure de calculer comment la lumière affecte les couleurs des fragments de nos objets. Dans les chapitres suivants, nous étudierons plus profondément ce que l’on peut faire avec ces modèles d’éclairage.

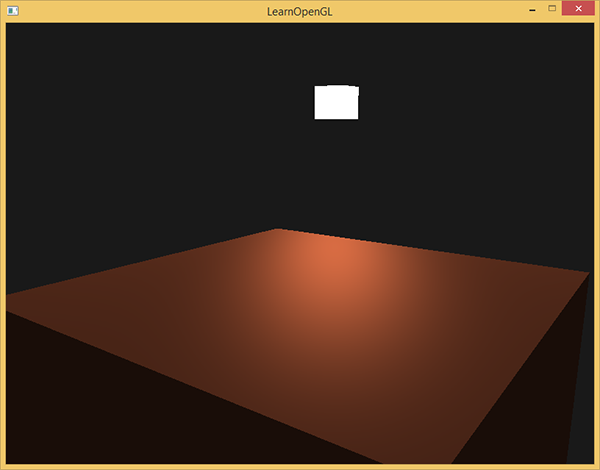
• Jusqu’à présent, la source de lumière était statique. Essayez de déplacer cette source autour de la scène, le résultat vous donnera un bon aperçu du modèle d’éclairage de Phong : solution.
• Modifiez les intensités des composantes ambiante, diffuse et spéculaire et observez le résultat. Modifiez aussi le facteur de brillance. Essayez de comprendre l’influence de chaque paramètre.
• Codez le modèle de Phong dans l’espace de vue plutôt que dans l’espace monde : solution.
• Implémentez le modèle de Gouraud à la place du modèle de Phong. Vous devriez voir une lumière moins précise (en particulier la composante spéculaire). Essayez de comprendre pourquoi vous obtenez un résultat étrange : solution.

Ce tutoriel est une traduction réalisée par Jean-Michel Fray dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.