V. Sources de lumières▲
Les éclairages utilisés jusqu’ici provenaient d’une source unique concentrée en un point de l’espace. Cela donne de bons résultats, mais dans le monde réel, on trouve différents types de sources lumineuses qui ont des effets divers. Une source qui projette de la lumière sur les objets est appelée un projecteur (light caster). Dans ce chapitre, nous verrons différents types de projecteurs. Apprendre à simuler différentes sources de lumière est encore un outil supplémentaire pour enrichir vos scènes.
Nous verrons d’abord les sources directionnelles, puis les sources ponctuelles qui en sont une extension et finalement nous parlerons des spots lumineux. Dans le chapitre suivant, nous combinerons ces différents types d’éclairages dans une seule scène.
V-A. Sources directionnelles▲
Lorsqu’une source est très éloignée, les rayons lumineux qui proviennent de cette source sont pratiquement parallèles. Tout se passe comme si les rayons arrivaient dans la même direction, quelles que soient la position de l’objet et celle du spectateur. Quand une source est modélisée comme infiniment éloignée, on parle de source directionnelle, car les rayons lumineux arrivent tous dans la même direction, indépendamment de la position de la source.
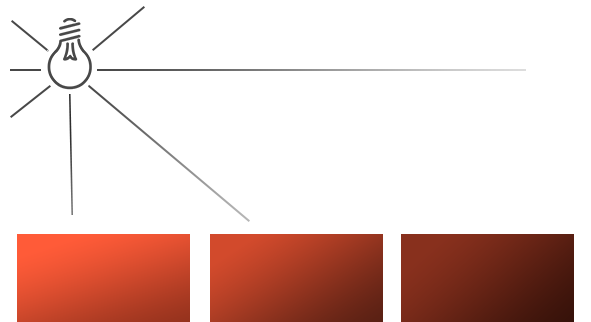
Un bon exemple d’une telle source est le soleil, qui n’est pas infiniment loin, mais si loin que tout se passe comme si c’était le cas. Les rayons lumineux provenant du soleil sont modélisés comme étant parallèles comme on le voit sur la figure suivante :

Puisque les rayons sont parallèles, la position de l’objet par rapport à la source est sans importance, la direction de la lumière est la même pour tous les objets de la scène. Les calculs d’éclairage seront donc similaires pour chaque objet.
On modélise une source directionnelle en définissant un vecteur direction au lieu d’un vecteur de position. Les calculs dans les shaders sont les mêmes, mais on utilisera cette fois la direction de la lumière au lieu de calculer le vecteur lightDir avec la position de la source :
struct Light {
// vec3 position; // inutile pour une source directionnelle
vec3 direction;
vec3 ambient;
vec3 diffuse;
vec3 specular;
};
…
void main()
{
vec3 lightDir = normalize(-light.direction);
…
}Noter que nous inversons le vecteur light.direction. Les calculs d’éclairage réalisés jusqu’à présent définissaient la direction de la lumière du fragment vers la source, mais les gens préfèrent généralement spécifier une lumière directionnelle avec une direction provenant de la source. Voilà pourquoi nous inversons le vecteur direction, afin qu’il pointe vers la source. N’oublions pas de normaliser ce vecteur, ce qui évite de supposer ce vecteur comme étant unitaire.
Le vecteur lightDir résultant est ensuite utilisé comme précédemment dans les calculs d’éclairage ambiant et diffus.
Pour montrer clairement qu’une source directionnelle produit le même effet sur tous les objets, nous reprenons la scène de la fin du neuvième chapitre sur les systèmes de coordonnées. Si vous n’avez pas étudié cette partie, nous avons défini dix positions différentes pour le même conteneur et généré une matrice de modèle par conteneur afin de définir la position de chacun d’entre eux au moyen d’une transformation de l’espace local vers l’espace monde
for(unsigned int i = 0; i < 10; i++)
{
glm::mat4 model;
model = glm::translate(model, cubePositions[i]);
float angle = 20.0f * i;
model = glm::rotate(model, glm::radians(angle), glm::vec3(1.0f, 0.3f, 0.5f));
lightingShader.setMat4("model", model);
glDrawArrays(GL_TRIANGLES, 0, 36);
}N’oublions pas de définir la direction de la source (noter que nous la définissons comme provenant de la source ; on voit que la direction de la lumière pointe vers le bas) :
lightingShader.setVec3("light.direction", -0.2f, -1.0f, -0.3f);Nous avons utilisé des vecteurs vec3 pour la position et la direction, mais certains préfèrent n’utiliser que des types vec4. Si l’on utilise des types vec4, il est important d’initialiser la composante w à la valeur 1.0, pour que les translations et les projections soient correctement effectuées. Cependant, pour un vecteur direction défini par un type vec4, nous ne voulons pas que les translations aient le moindre effet, et dans ce cas il faudra initialiser la composante w à 0.0.
Les vecteurs direction sont représentés comme suit : vec4(0.2f, 1.0f, 0.3f, 0.0f). Cela peut aussi servir de test pour le type de source lumineuse : si la composante w vaut 1.0, nous avons un vecteur de position pour la source, alors que si w vaut 0.0, nous avons un vecteur de direction ; on peut ajuster nos calculs en se basant sur cette valeur :
if(lightVector.w == 0.0) // note: attention aux erreurs de calculs pour les réels
// Calculs pour une source directionnelle
else if(lightVector.w == 1.0) // Calculs tenant compte de la position de la sourceAnecdote : c’est vraiment comme cela que l’ancien OpenGL (pipeline fixe) déterminait si une source lumineuse était directionnelle ou non et ajustait les calculs d’éclairage en fonction.
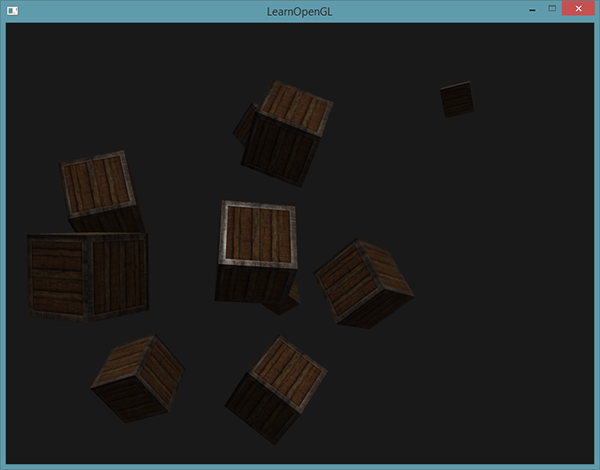
Si vous compilez l’application et observez la scène, on a l’impression que les objets sont éclairés par une source lumineuse comme un soleil. Notez que les composantes diffuses et spéculaires se comportent comme s’il y avait une source lumineuse dans le ciel. Voilà ce que ça donne :
Le code complet se trouve ici.
V-B. Sources ponctuelles▲
Les sources directionnelles sont parfaites pour la lumière qui éclaire la scène entière, mais à part cela on souhaitera aussi disposer de sources ponctuelles réparties dans la scène. Une source ponctuelle est une source de lumière placée à une position précise et qui éclaire dans toutes les directions, l’intensité des rayons lumineux s’atténuant avec la distance à la source. C’est le cas des ampoules et des bougies, qui sont des sources ponctuelles.
Dans les premiers chapitres, nous avons travaillé avec une source ponctuelle (très simple). Nous avions une source de lumière à une position donnée qui émettait de la lumière dans toutes les directions à partir de cette position. Cependant, cette source simulait des rayons sans atténuation, comme si elle était très puissante. Dans la plupart des simulations 3D, nous voudrons des sources qui n’éclairent qu’une partie de la scène, proche de la source, et non la scène entière.
Si vous ajoutez les dix conteneurs à la scène éclairée du chapitre précédent, vous verrez que le conteneur du fond est éclairé avec la même intensité que celui du premier plan ; on n’a pas défini de formule pour diminuer l’intensité de la lumière avec la distance. Nous voudrions que le conteneur du fond soit bien moins éclairé que ceux se trouvant près de la source lumineuse.
V-B-1. Atténuation▲
La diminution de l’intensité de la lumière en fonction de la distance qu’un rayon lumineux parcourt se nomme atténuation. À cette fin, on pourrait simplement utiliser une fonction linéaire. Les objets éloignés seraient moins éclairés que les objets proches. Cependant, une fonction linéaire donnerait un résultat peu crédible. En réalité, les éclairages donnent une lumière assez forte quand on est près de la source, mais qui diminue assez rapidement lorsque l’on s’éloigne, puis s’atténue moins vite pour des distances plus grandes. Il nous faut donc une fonction différente pour rendre compte de l’atténuation.
Par chance, ce phénomène a déjà été modélisé. La formule suivante calcule l’atténuation en fonction de la distance entre le fragment et la source, valeur que l’on multipliera par le vecteur intensité de la lumière :
kitxmlcodelatexdvpF_{att} = \frac{1.0}{K_c + K_l * d + K_q * d²}finkitxmlcodelatexdvpDans cette formule, kitxmlcodeinlinelatexdvpdfinkitxmlcodeinlinelatexdvp est la distance entre le fragment et la source. Ensuite, on définit 3 paramètres (configurables) :
- Le paramètre constant kitxmlcodeinlinelatexdvpK_cfinkitxmlcodeinlinelatexdvp est conservé à la valeur 1.0, son rôle est d’assurer que le dénominateur est toujours supérieur à 1, sinon la lumière risquerait d’être plus forte que la source, ce qui n’est pas possible.
- Le terme linéaire kitxmlcodeinlinelatexdvpK_l * dfinkitxmlcodeinlinelatexdvp réduit la lumière de façon linéaire avec la distance.
- Le terme quadratique kitxmlcodeinlinelatexdvpK_g * d^2finkitxmlcodeinlinelatexdvp réduit la lumière avec le carré de la distance. Ce terme est moins significatif que le terme linéaire quand la distance est faible, mais devient prépondérant si la distance augmente.
Du fait de ce terme quadratique, la lumière diminue linéairement pour des distances faibles, puis beaucoup plus vite pour des distances plus grandes. Le résultat est ainsi conforme à ce que l’on souhaite. La courbe suivante montre l’effet de l’atténuation sur une distance de 100 :
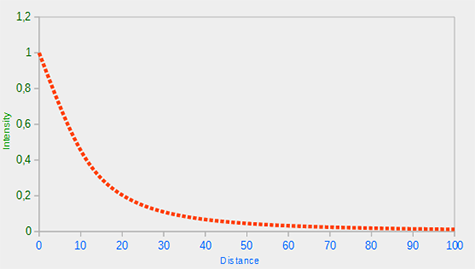
On voit que l’intensité est élevée pour de faibles distances, mais qu’elle diminue rapidement avec la distance pour tendre lentement vers 0. C’est bien ce que nous voulons.
V-B-2. Choisir les bonnes valeurs▲
Comment choisir ces paramètres d’atténuation ? Cela dépend de nombreux facteurs : l’environnement, la distance que vous voulez couvrir avec votre lampe, le type de lumière, etc. Dans la plupart des cas, c’est une question d’expérience et d’ajustements. Le tableau suivant donne des valeurs pour simuler des éclairages réalistes qui couvrent une certaine distance. La première colonne indique la distance couverte par la lampe, les autres colonnes indiquent les paramètres. Ces valeurs constituent un bon point de départ pour la plupart des lampes, merci au wiki d’Ogre3D :
|
Distance |
Constant |
Linéaire |
Quadratique |
|
7 |
1.0 |
0.7 |
1.8 |
|
13 |
1.0 |
0.35 |
0.44 |
|
20 |
1.0 |
0.22 |
0.20 |
|
32 |
1.0 |
0.14 |
0.07 |
|
50 |
1.0 |
0.09 |
0.032 |
|
65 |
1.0 |
0.07 |
0.017 |
|
100 |
1.0 |
0.045 |
0.0075 |
|
160 |
1.0 |
0.027 |
0.0028 |
|
200 |
1.0 |
0.022 |
0.0019 |
|
325 |
1.0 |
0.014 |
0.0007 |
|
600 |
1.0 |
0.007 |
0.0002 |
|
3250 |
1.0 |
0.0014 |
0.000007 |
Le terme constant est fixé à 1.0 dans tous les cas. Le terme linéaire kitxmlcodeinlinelatexdvpK_lfinkitxmlcodeinlinelatexdvp est assez petit pour couvrir de grandes distances, et le terme quadratique est encore plus faible. Testez ces valeurs pour voir leur effet dans votre application. Dans notre cas, une distance de 32 à 100 est correcte pour la plupart des lampes.
V-B-3. Implémenter l’atténuation▲
Pour implémenter l’atténuation, il nous faudra trois valeurs supplémentaires dans le fragment shader pour les trois paramètres de la formule précédente. Le mieux est de les placer dans la structure dont nous disposons. Nous calculons lightDir comme dans le chapitre précédent, et non comme au début de celui-ci pour les sources directionnelles.
struct Light {
vec3 position;
vec3 ambient;
vec3 diffuse;
vec3 specular;
float constant;
float linear;
float quadratic;
};Nous initialisons ces valeurs dans l’application, en choisissant pour la source de couvrir une distance de 50, le tableau nous donne les valeurs des paramètres d’atténuation :
lightingShader.setFloat("light.constant", 1.0f);
lightingShader.setFloat("light.linear", 0.09f);
lightingShader.setFloat("light.quadratic", 0.032f);Coder l’atténuation dans le fragment shader est assez direct : on calcule simplement la valeur de l’atténuation au moyen de la formule et on multiplie par les composantes ambiante, diffuse et spéculaire.
Dans cette formule, nous avons besoin de la distance à la source ; il faut se rappeler comment on calcule la longueur d’un vecteur. Il faut calculer la différence entre le vecteur position de la source et le vecteur position du fragment, et utiliser la norme de ce vecteur. On utilise la fonction GLSL length() à cet effet :
float distance = length(light.position – FragPos);
float attenuation = 1.0 / (light.constant + light.linear * distance + light.quadratic * (distance * distance));Ensuite, nous ajoutons cette valeur d’atténuation aux calculs d’éclairage.
On pourrait ne pas inclure la composante ambiante dans ce calcul, en supposant que la lumière ambiante n’est pas concernée par l’atténuation, mais si on utilise plusieurs sources, les composantes ambiantes s’accumuleraient, ce qui n’est pas souhaitable. À vous de voir ce qui est le mieux dans votre environnement.
ambient *= attenuation;
diffuse *= attenuation;
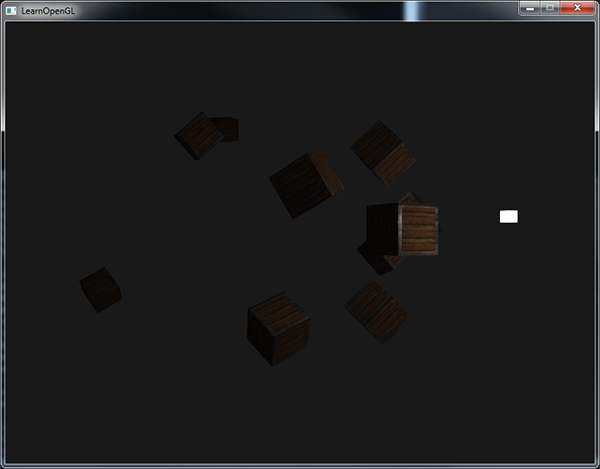
specular *= attenuation;En lançant l’application, on obtient ceci :
On voit que seuls les conteneurs de premier plan sont éclairés, le plus proche étant le plus lumineux. Les conteneurs du fond sont assez sombres, car ils sont trop loin de la source. Vous trouverez le code source ici.
Une source ponctuelle est donc une source de lumière située en un point précis et dont la lumière faiblit avec la distance. Voyons encore un autre type de source de lumière.
V-C. Spot lumineux▲
Un spot est une source placée à un endroit précis de la scène, mais qui n’éclaire que dans une seule direction. Seuls les objets situés dans un cône de lumière sont éclairés, le reste ne l’étant pas. Un bon exemple est un lampadaire de rue ou encore un flash d’appareil photo.
Un spot dans OpenGL est représenté par une position dans l’espace monde, une direction et un angle qui spécifie l’ouverture du cône de lumière. Pour chaque fragment, on calcule si le fragment se trouve dans le cône de lumière et dans ce cas, on tient compte de cette source pour l’éclairage du fragment. La figure suivante montre le principe de ce type de source :
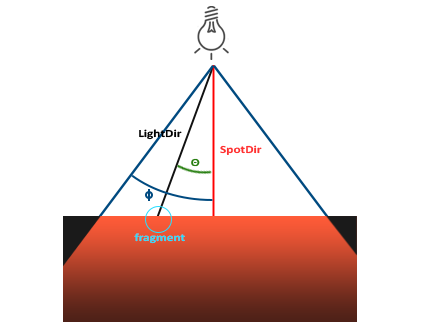
- LightDir : le vecteur allant du fragment à la source.
- SpotDir : la direction dans laquelle pointe le spot.
- Phi ϕ : l’angle d’ouverture du cône de lumière. En dehors de ce cône, point d’éclairage depuis le spot.
- Theta θ : l’angle entre le vecteur LightDir et le vecteur SpotDir. θ doit être inférieur à Φ pour que le fragment soit éclairé.
Nous calculerons le produit scalaire entre le vecteur LightDir et le vecteur SpotDir afin de trouver θ, puis de le comparer à ϕ. Maintenant que vous avez compris ce qu’est un spot, nous allons en créer un sous forme de lampe frontale.
V-D. Lampe frontale▲
Une lampe frontale est un spot positionné comme le spectateur et destiné à avoir la même perspective que lui. Une lampe frontale est donc un spot classique, mais sa position et sa direction sont continuellement mises à jour en fonction de la position et de l’orientation de spectateur.
Les valeurs nécessaires pour les calculs dans le fragment shader sont le vecteur position du spot (pour calculer le vecteur direction de la lumière) le vecteur de direction du spot et l’angle d’ouverture. On peut placer ces valeurs dans la structure Light :
struct Light {
vec3 position;
vec3 direction;
float cutOff;
…
};Nous passons les bonnes valeurs au shader :
lightingShader.setVec3("light.position", camera.Position);
lightingShader.setVec3("light.direction", camera.Front);
lightingShader.setFloat("light.cutOff", glm::cos(glm::radians(12.5f)));On peut remarquer que nous ne mémorisons pas l’angle du cône, mais passons directement le cosinus de cet angle au fragment shader. En effet, dans le fragment shader, nous utilisons le produit scalaire entre le vecteur LightDir et le vecteur SpotDir, nous trouvons ainsi le cosinus de l’angle formé par ces deux vecteurs, et non pas l’angle lui-même. Pour calculer l’angle, il faudrait utiliser la fonction inverse de cosinus, ce qui est une opération coûteuse. Il est plus efficace de calculer le cosinus de l’angle Φ et de comparer les deux valeurs de cosinus, et de déterminer si le fragment est éclairé ou non :
float theta = dot(lightDir, normalize(-light.direction));
if(theta > light.cutOff)
{
// calculs d’éclairement
}
else // sinon, utiliser la lumière ambiante pour les parties de la scène non éclairées par le spot
color = vec4(light.ambient * vec3(texture(material.diffuse, TexCoords)), 1.0);Nous calculons d’abord le produit scalaire entre le vecteur lightDir et l’opposé du vecteur direction (les deux vecteurs doivent pointer vers la source). Attention à normaliser tous ces vecteurs.
Pourquoi utiliser le signe > et non le signe < pour le test des angles ? N’oublions pas que nous utilisons le cosinus des angles, dont la courbe représentative est figurée ci-après :
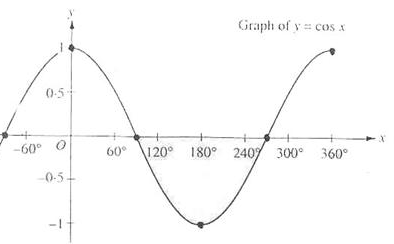
Entre 0° et 90°, la fonction cosinus est décroissante, il faut inverser le signe de la comparaison.
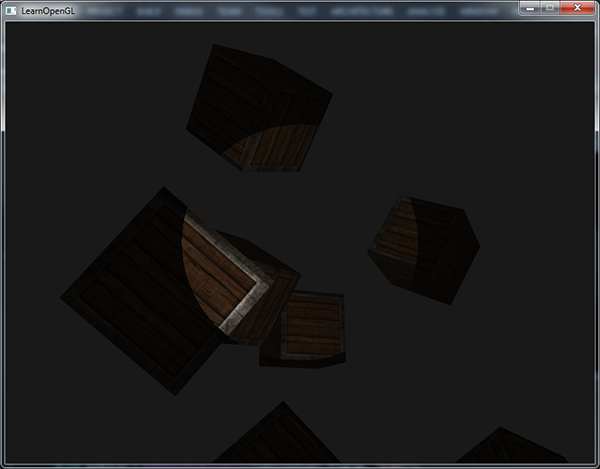
L’application résulte en un spot lumineux qui n’éclaire que les fragments situés dans le cône de lumière :
Vous trouverez le code ici.
Mais le résultat semble encore un peu artificiel, car les bords du cône de lumière sont trop nets. Un fragment qui se trouve au bord du cône de lumière n’est pas du tout éclairé, au lieu de recevoir un peu de lumière. Un spot réaliste doit donner des bords où la lumière diminue en douceur.
V-E. Atténuation des bords▲
Pour créer un spot dont les bords donnent une lumière atténuée, nous simulerons un spot ayant un cône interne et un cône externe. Le cône interne est celui défini précédemment ; pour le cône externe, la lumière doit diminuer progressivement jusqu’à l’extérieur de ce cône.
Pour ce nouveau cône, nous définissons (par son cosinus) un angle γ donnant la mesure entre la direction du spot et le vecteur du cône extérieur. Si un fragment est dans le cône externe, mais pas dans le cône interne, nous calculerons une intensité entre 0.0 et 1.0. Dans le cône interne, l’intensité sera égale à 1.0 et à 0.0 au-delà du cône extérieur.
On peut calculer cette intensité par la formule suivante :
kitxmlcodelatexdvpI = \frac{\theta - \gamma}{\epsilon}finkitxmlcodelatexdvpOù kitxmlcodeinlinelatexdvp\epsilonfinkitxmlcodeinlinelatexdvp est le cosinus entre le cône interne (kitxmlcodeinlinelatexdvp\phifinkitxmlcodeinlinelatexdvp) et le cône externe (kitxmlcodeinlinelatexdvp\gammafinkitxmlcodeinlinelatexdvp) (kitxmlcodeinlinelatexdvp\epsilon = \phi - \gammafinkitxmlcodeinlinelatexdvp. Le résultat kitxmlcodeinlinelatexdvpIfinkitxmlcodeinlinelatexdvp est l’intensité du spot pour un fragment donné.
Il est un peu difficile de comprendre cette formule, voyons quels résultats on obtient pour quelques valeurs d’angles :
|
θ |
θ |
ϕ |
Φ |
γ |
γ |
ϵ |
I |
|
0.87 |
30 |
0.91 |
25 |
0.82 |
35 |
0.91 - 0.82 = 0.09 |
0.87 - 0.82 / 0.09 = 0.56 |
|
0.9 |
26 |
0.91 |
25 |
0.82 |
35 |
0.91 - 0.82 = 0.09 |
0.9 - 0.82 / 0.09 = 0.89 |
|
0.97 |
14 |
0.91 |
25 |
0.82 |
35 |
0.91 - 0.82 = 0.09 |
0.97 - 0.82 / 0.09 = 1.67 |
|
0.83 |
34 |
0.91 |
25 |
0.82 |
35 |
0.91 - 0.82 = 0.09 |
0.83 - 0.82 / 0.09 = 0.11 |
|
0.64 |
50 |
0.91 |
25 |
0.82 |
35 |
0.91 - 0.82 = 0.09 |
0.64 - 0.82 / 0.09 = -2.0 |
|
0.966 |
15 |
0.9978 |
12.5 |
0.953 |
17.5 |
0.9978 - 0.953 = 0.0448 |
0.966 - 0.953 / 0.0448 = 0.29 |
C’est une interpolation entre les limites des deux cônes, basée sur l’angle θ. Si vous ne voyez pas bien comment cela fonctionne, pas d’inquiétude, vous pouvez utiliser la formule telle quelle, et y revenir plus tard.
Puisque nous avons une intensité qui devient négative en dehors du cône extérieur et plus grande que 1 dans le cône interne, nous allons limiter les valeurs au moyen de la fonction clamp(). Il suffit ensuite d’utiliser cette nouvelle valeur d’intensité :
float theta = dot(lightDir, normalize(-light.direction));
float epsilon = light.cutOff – light.outerCutOff;
float intensity = clamp((theta - light.outerCutOff) / epsilon, 0.0, 1.0);
…
// nous conservons la lumière ambiante pour avoir un peu de lumière en dehors du cône du spot
diffuse *= intensity;
specular *= intensity;N’oublions pas d’ajouter le champ outerCutOff à la structure et d’affecter cette valeur uniforme dans l’application. Pour l’image suivante, nous avons choisi un angle interne de 12,5° et un angle externe de 17,5° :
Ah, c’est bien meilleur ! Jouez avec les angles internes et externes et créez un spot qui vous conviendra pour le mieux. Vous trouverez le code source ici.
Une lampe frontale de ce type est parfaite pour les jeux d’horreur et combinée avec des sources directionnelles et des sources ponctuelles, le résultat sera très réaliste. Dans le prochain chapitre, nous combinerons toutes ces lampes et ces astuces.
V-F. Exercices▲
- Essayez les différents types d’éclairages et leur fragment shader. Essayez d’inverser certains vecteurs et changez < en >. Interprétez les images obtenues.
V-G. Remerciements▲
Ce tutoriel est une traduction réalisée par Jean-Michel Fray dont l’original a été écrit par Joey de Vries et qui est disponible sur le site Learn OpenGL.